CS61B学习笔记(四)--Reading2.1-列表-海象之谜

什么是海象之谜?

尝试预测当我们运行下面的代码时会发生什么。更改为 b 会影响 a 吗，更改为 x 会影响 y 吗？提示：如果你来自 Python，Java 也有相同的行为。

public class PollQuestions {
    public static void main(String[] args) {
        Walrus a = new Walrus(1000, 8.3);
        Walrus b;
        b = a;
        b.weight = 5;
        System.out.println(a);
        System.out.println(b);

        int x = 5;
        int y;
        y = x;
        x = 2;
        System.out.println("x is: " + x);
        System.out.println("y is: " + y);
    }

    public static class Walrus {
        public int weight;
        public double tuskSize;

        public Walrus(int w, double ts) {
            weight = w;
            tuskSize = ts;
        }

        public String toString() {
            return String.format("weight: %d, tusk size: %.2f", weight, tuskSize);
        }
    }
}

答案:

位

计算机中的所有信息都以 1 和 0 的序列形式存储在内存中。一些例子：

• 72 通常存储为 01001000
• 205.75 通常存储为 01000011 01001101 11000000 00000000
• 字母 H 通常存储为 01001000（与 72 相同）
• 真实值通常存储为00000001

一个有趣的观察结果是，72 和 H 都存储为 01001000。这就提出了一个问题：一段 Java 代码如何知道如何解释 01001000？

答案是通过类型

声明变量（简体）

您可以将计算机视为包含大量用于存储信息的内存位，每个内存位都有一个唯一的地址。现代计算机可以使用数十亿个这样的比特。

当你声明某种类型的变量时，Java 会找到一个连续的块，该块的位恰好足够容纳该类型的事物。例如，如果声明一个 int，则会得到一个 32 位的块。如果声明一个字节，则会得到一个 8 位的块。Java 中的每种数据类型都包含不同数量的位。在这个类中，确切的数字对我们来说并不是很重要。

为了方便的比喻，我们将其中一个块称为比特的“盒子”。

除了留出内存之外，Java 解释器还在内部表中创建一个条目，该条目将每个变量名称映射到框中第一个位的位置。

例如，如果声明 int x 了 和 double y ，则 Java 可能会决定使用计算机内存的 352 到 384 位来存储 x，并使用 20800 到 20864 位来存储 y。然后，解释器将记录 int x 从位 352 开始，y 从位 20800 开始。例如，在执行代码后：

int x;
double y;

我们最终会得到尺寸为 32 和 64 的盒子，如下图所示：

声明变量时，Java 不会将任何内容写入保留框中。换句话说，没有默认值。因此，Java 编译器会阻止您使用变量，直到使用 = 运算符将位填充到框中。出于这个原因，我避免在上图的框中显示任何位。

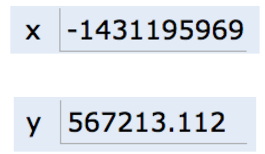
当您为内存盒赋值时，它将填充您指定的位。例如，如果我们执行以下行：

x = -1431195969;
y = 567213.112;

简化的框表示法

虽然我们在上一节中使用的框表示法对于理解引擎盖下发生的事情非常有用，但它对实际目的没有用，因为我们不知道如何解释二进制位。

因此，我们将用人类可读的符号来编写它们，而不是用二进制文件编写内存盒内容。我们将在课程的其余部分这样做。例如，在执行以下操作后：

int x;
double y;
x = -1431195969;
y = 567213.112;

我们可以使用我称之为简化框表示法来表示程序环境，如下所示：

黄金平等法则 （GRoE）

现在有了简化的盒子符号，我们终于可以开始解开海象之谜了。

事实证明，我们的 Mystery 有一个简单的解决方案：当你编写 y = x 时，你告诉 Java 解释器将 x 中的位复制到 y 中。在理解我们的海象之谜时，这条平等的黄金法则 （GRoE） 是所有真理的根源。

int x = 5;
int y;
y = x;
x = 2;
System.out.println("x is: " + x);
System.out.println("y is: " + y);

因此，Java的复制操作是复制位

引用类型

上面，我们说了 8 种原始类型：byte、short、int、long、float、double、boolean、char。其他所有内容，包括数组，都不是原始类型，而是 reference type .

当我们使用 new （例如 Dog、Walrus、Planet）实例化一个 Object 时，Java 首先为类的每个实例变量分配一个框，并用默认值填充它们。然后，构造函数通常（但并非总是）用其他值填充每个框。

引用类型可能都需要new，这可能意味着引用变量声明的其实是类似于cpp中的指针?

引用变量声明

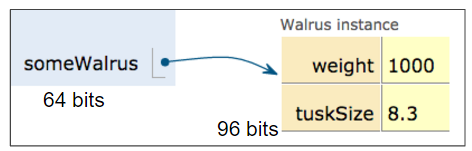
当我们声明任何引用类型（Walrus、Dog、Planet、数组等）的变量时，无论什么类型的对象，Java 都会分配一个 64 位的盒子。

乍一看，这似乎导致了海象悖论。上一节中的 Walrus 需要超过 64 位来存储。此外，无论对象的类型如何，我们只能获得 64 位来存储它，这似乎很奇怪。

但是，通过以下信息可以轻松解决此问题：64 位框不包含有关海象的数据，而是内存中海象的地址。

类似cpp中的指针，指针变量存储的是指针指向的地址，通常只有4个字节；而指针所指向的那个地址不一定存储了4个字节。

框和指针表示法

和以前一样，很难解释引用变量中的一堆位，因此我们将为引用变量创建一个简化的框表示法，如下所示：

• 如果一个地址全为零，我们将用 null 表示它。
• 非零地址将由指向对象实例化的箭头表示。

这有时也称为“框和指针”表示法。

对于上一节中的示例，我们将有：

参数传递

当您将参数传递给函数时，您也只是在复制位。换言之，GRoE 也适用于参数传递。复制位通常称为“按值传递”。在 Java 中，我们总是按值传递。

例如，请考虑以下函数：

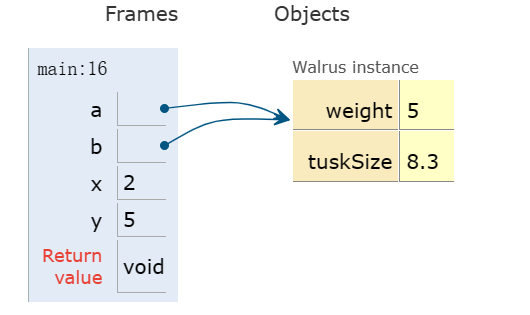
public static double average(double a, double b) {
    return (a + b) / 2;
}

假设我们调用这个函数，如下所示：

public static void main(String[] args) {
    double x = 5.5;
    double y = 10.5;
    double avg = average(x, y);
}

实际上我们是将x，y的值拷贝给了a, b。

列表的实例化

如上所述，存储数组的变量是引用变量，就像任何其他变量一样。例如，请考虑以下声明：

int[] x;
Planet[] planets;

这两个声明都创建了 64 位的内存盒。 x 只能保存数组的地址，并且 planets 只能保存 Planet int 数组的地址。

实例化数组与实例化对象非常相似。例如，如果我们创建一个大小为 5 的整数数组，如下所示：

x = new int[]{0, 1, 2, 95, 4};

然后，关键字 new 创建 5 个框，每个框 32 位，并返回整个对象的地址以分配给 x。

破碎的被褥法则

https://readit.site/a/9amjk

数学天花板：你的认知突破点在哪里？– 糟糕的图纸数学 — The Math Ceiling: Where’s your cognitive breaking point? – Math with Bad Drawings

我感觉这个很有意思:

	在大学里，我和我的室友从一些朋友那里买了一个二手被褥。他们住在一楼;我们住在四楼。他们很好心，他们帮我们抬上楼梯。
	当他们登上三楼的平台时，他们听到了一声裂缝。一根小小的金属棒从被褥上折断了。我们都检查了一下，但甚至不知道这件作品是从哪里来的。由于被褥看起来很好，我们只是耸了耸肩。
	在我们的房间里呆了一个星期后，被褥开始下垂。“它总是这样吗？”我们互相问。
	一个月后，它尴尬地下垂了。坐在最后，沙发的曲率会把你（和其他人）扔进一个中央的猪堆里。
到学期结束时，它已经倒在尘土飞扬的宿舍地板上，这是曾经繁荣的被褥的破碎骨架。
	现在，宜家家具是客厅的果蝇：出了名的短命。毫无疑问，我们的被褥寿命是有上限的，也许是三四年。但这一个只活了八个月。
	事后看来，很明显，破碎的碎片绝对至关重要。没有它被褥似乎很好。但日复一日，随着每一个新的屁股，重量都压在结构的某些部分上，从来都不意味着独自承受负载。框架变得扭曲。压力不可持续地增加。被褥的内部时钟默默地滴答作响，直到缺乏支持被证明是压倒性的，整个事情都崩溃了。
	而且，可悲的是，数学课也是如此。
	假设你正在读八年级。您可以以完美的流动性和精度绘制线性方程。您可以计算它们的斜率、识别点并生成平行线和垂直线。
	但是，如果你缺少一个简单的理解——这些图只是满足方程的 x-y 对——那么你就是一个破碎的被褥。你错过了未来学习至关重要的一块。二次函数会困扰你;正弦曲线永远不会有意义;你可能会在微积分之后保释，安慰自己，“好吧，至少我的上限比一些人高。
	你可能会问，“既然我现在很好，难道我不能在以后真正需要的时候添加缺失的部分吗？有时，是的。但这要困难得多。你现在已经花了好几年时间没有这个关键的部分。你已经开发了捷径和零敲碎打的方法来度过难关。这些工作了一段时间，但它们扭曲了框架，现在你来了。为了继续前进，你必须忘记你的变通方法--有效地将被褥弯曲回原来的形状--然后才能继续。但是，放弃让你走到这一步的策略几乎是不可能的。
	稍后添加缺失的部分意味着要等到损坏已经开始，并且很难挽回。
	我相信，这是许多学生所经历的天花板。这不是他们神经病学的固有局限性。这是我们创造的东西。我们通过言语或行动说：“你不明白也没关系。只需按照以下步骤操作，并在后面检查您的答案。我们通过说“只有聪明的人才能得到它;至于其余的，我只想确保他们能做到。我们通过说，“好吧，他们现在不明白，但他们最终会自己弄清楚。
	这样一来，我们就可以成功地把被褥弄上楼梯。但在这个过程中会丢失一些东西。在没有关键理解的情况下将我们的学生送上前方，就像在没有替换弹药的情况下将他们送上战场一样。当然，他们会发射几发子弹，但当他们意识到缺少一些东西时，恢复为时已晚。

一时半解虽然这在短期内可能很好，但从长远来看，在没有完全理解的情况下做问题可能会注定你以后会失败。有一篇关于这个所谓的破碎被褥法则的博客文章，你可能会觉得很有趣。

IntLists

事实证明，一个非常基本的列表实现起来是微不足道的，如下所示：

实现起来其实类似于”链表”

public class IntList {
    public int first;
    public IntList rest;        

    public IntList(int f, IntList r) {
        first = f;
        rest = r;
    }
    
    /** Return the size of the list using... recursion! */
    public int size() {
        if (rest == null) {
            return 1;
        }
        return 1 + this.rest.size();
    }
    
    /** Return the size of the list using no recursion! */
    public int iterativeSize() {
        IntList p = this;
        int totalSize = 0;
        while (p != null) {
            totalSize += 1;
            p = p.rest;
        }
        return totalSize;
    }
    
    /** Returns the ith item of this IntList*/
    public int get(int i){
        if (i == 0) {
            return first;
        }
        return rest.get(i - 1);
    }
}