CS61B学习笔记(十三)-Rd10-ADP、树
Slides:cs61b 2020 lec16 ds2 adts, sets, maps, binary search trees - Google 幻灯片
Reading:10.2 Trees · Hug61B (gitbooks.io)
ADTs
抽象数据类型(ADT)仅通过其操作进行定义,而不是通过其实现。
这意味着ADT定义了一组操作或行为,而不涉及具体的实现细节。
例如,在proj1a中,我们开发了一个ArrayDeque和一个LinkedListDeque,它们具有相同的方法,但这些方法的编写方式非常不同。在这种情况下,我们说ArrayDeque和LinkedListDeque是Deque ADT的实现。从这个描述中,我们可以看出ADT和接口在某种程度上是相关的。
ADT强调的是数据和操作的抽象描述,而接口强调的是行为和操作的规范定义。
在概念上,Deque是一个接口,ArrayDeque和LinkedListDeque是其实现。在代码中,为了表达这种关系,我们让ArrayDeque和LinkedListDeque类从Deque接口继承。
一些常用的ADT包括:
栈(Stack):支持后进先出检索元素的结构
push(int x): 将x放在栈顶int pop(): 取出栈顶元素
列表(List)
: 一组有序的元素
add(int i): 添加一个元素int get(int i): 获取索引为i的元素
集合(Set)
: 一组无序的唯一元素(不重复)
add(int i): 添加一个元素contains(int i): 返回集合中是否包含该值的布尔值
映射(Map)
: 一组键/值对
put(K key, V value): 将一个键值对放入映射V get(K key): 获取与键对应的值
加粗的ADT是一个名为Collections的更大的总体接口的子接口
下面我们展示接口和类之间的关系。接口为白色,类为蓝色。
ADT使我们能够以高效而优雅的方式利用面向对象编程。您在proj1b中看到了我们如何交换OffByOne和OffByN比较器,因为它们都实现了相同的接口!同样,您可以交替使用ArrayDeque或LinkedListArrayDeque,因为它们都是Deque ADT的一部分。
在接下来的章节中,我们将致力于定义一些更多的ADT并列举它们的不同实现。
二叉查找树
现在我们要学习可能是有史以来最重要的数据结构之一。
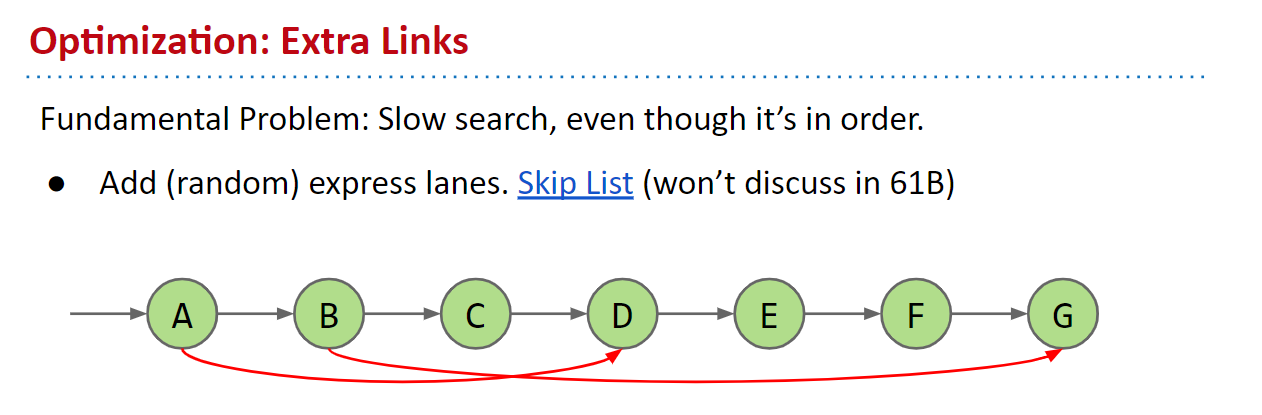
链表很棒,但是查找项需要很长时间,即使列表是排序的!如果项目在列表的末尾怎么办?那将花费线性时间!看一下下面的链表,并让自己相信这是真的。

我们知道,对于数组,我们可以使用二分查找来更快地找到元素。具体地说,时间复杂度是log(*n*)。关于二分查找的简短解释,请查看此链接。
TL;DR:在二分查找中,我们知道列表是排序的,因此我们可以利用这一信息来缩小搜索范围。首先,我们查看中间元素。如果它大于我们要查找的元素,则向左查找。如果它小于我们要查找的元素,则向右查找。然后,我们查看各自一半的中间元素,并重复此过程,直到找到我们要查找的元素(或因为列表不包含它而找不到)。
但是,我们如何在链表中运行二分查找呢?我们需要遍历到中间位置才能检查那里的元素,这本身就需要线性时间!
我们可以实现一种优化,即具有对中间节点的引用。这样,我们可以在常数时间内到达中间位置。然后,如果我们翻转节点的指针,这样就可以遍历到左右两半,从而将运行时间减半!

但是,我们可以做得更好。我们可以通过像下面这样在每个递归半部分的中间添加指针来进一步优化。

现在,如果你垂直拉伸这个结构,你会看到一棵树!
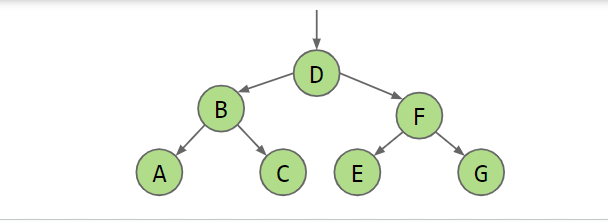
这棵具体的树称为二叉树,因为每个交叉点分为两个。
树的属性
让我们更加正式地定义树数据结构。
树由以下组成:
- 节点
- 将这些节点连接起来的边。
- 约束:任何两个节点之间只有一条路径。
在某些树中,我们选择一个根节点,这是一个没有父节点的节点。
树还有叶子节点,它们是没有子节点的节点。
下面的结构是有效的树:
练习 10.2.1:你能想出一个非有效的树的例子吗?
将这与我们之前提出的原始树结构联系起来,我们现在可以对已有的约束引入新的约束。这创建了更具体的树类型,其中两个示例是二叉树和二叉搜索树。
- 二叉树:除了上述要求外,还满足二进制属性约束。即每个节点只有0、1或2个子节点。
- 二叉搜索树:除了所有上述要求外,还具有以下属性:对于树中的每个节点X:
- 左子树中的每个键都小于X的键。
- 右子树中的每个键都大于X的键。记住这个属性!!我们在本模块和61B的整个持续时间中将引用它很多次。
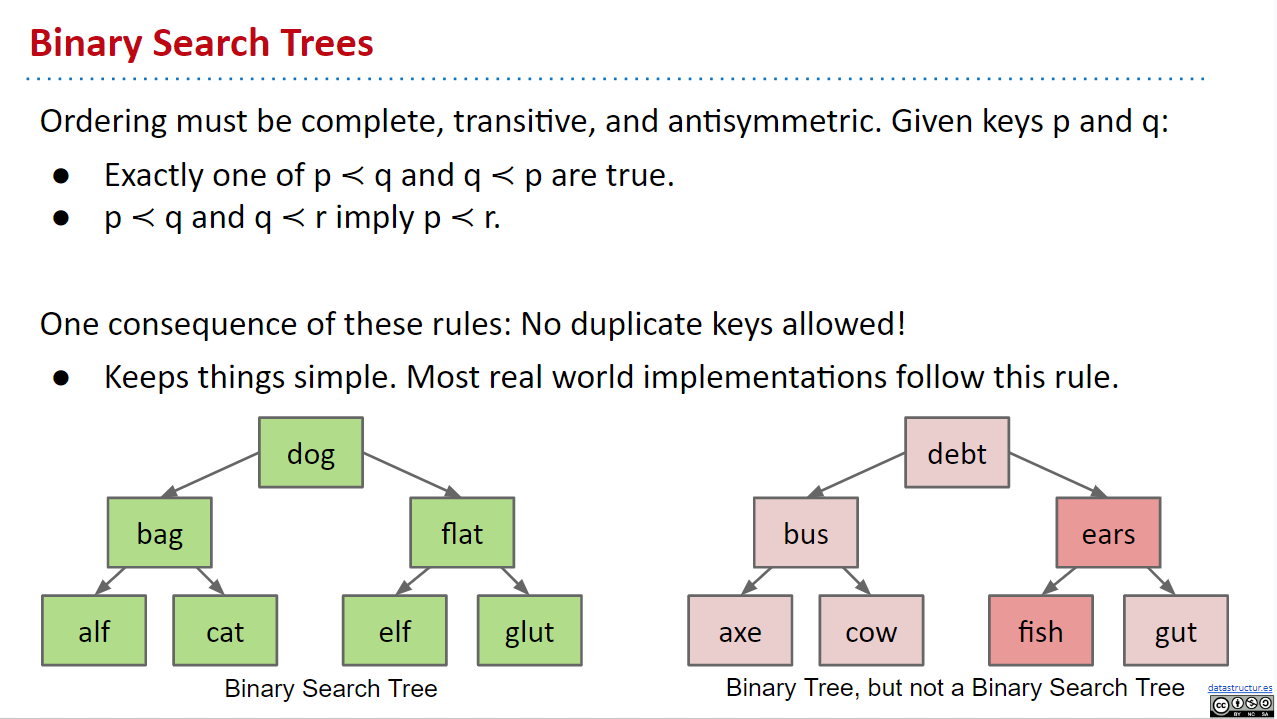
满足对称性和传递性
这是我们在本模块中将使用的BST类:
1 | private class BST<Key> { |
二叉搜索树操作
搜索
要搜索某个元素,我们使用二分查找,这在很大程度上是由于前一节中描述的BST属性的便利!
我们知道BST被构造得使得节点的右侧所有元素都大于节点,并且左侧所有元素都小于节点。基于此,我们可以从根节点开始,将其与我们正在查找的元素X进行比较。如果X大于根,则我们转向根的右子节点。如果X小于根,则我们转向根的左子节点。我们递归地重复这个过程,直到我们找到项目或者我们到达一个叶子节点,在这种情况下,树不包含该项目。
练习 10.2.2:尝试自己编写此方法。这是方法头:static BST find(BST T, Key key)。它应返回以与键参数匹配的键根节点。
1 |
|
如果我们的树相对“茂密”,那么find操作将在log(�)log(n)时间内运行,因为树的高度是logn,这相当快!
插入
我们总是在叶子节点插入!
首先,我们在树中搜索节点。如果我们找到它,则不做任何操作。如果我们找不到它,则我们已经在叶子节点上。此时,我们只需将新元素添加到叶子的左侧或右侧,保持BST属性不变。
练习 10.2.3:尝试自己编写此方法。这是方法头:static BST insert(BST T, Key ik)。它应返回插入了正确位置的新节点的完整BST。
1 | static BST insert(BST T, Key ik) { |
练习 10.2.4:想出一种插入顺序,会导致树的高度不同。尝试找到树高度的两种极端情况。提示:您的第一个插入将决定随后插入的行为。
删除
从二叉树中删除节点稍微复杂一些,因为每当我们删除时,我们都需要确保重构树并仍然保持其BST属性。
让我们将此问题分为三个类别:
- 我们尝试删除的节点没有子节点
- 有一个子节点
- 有两个子节点
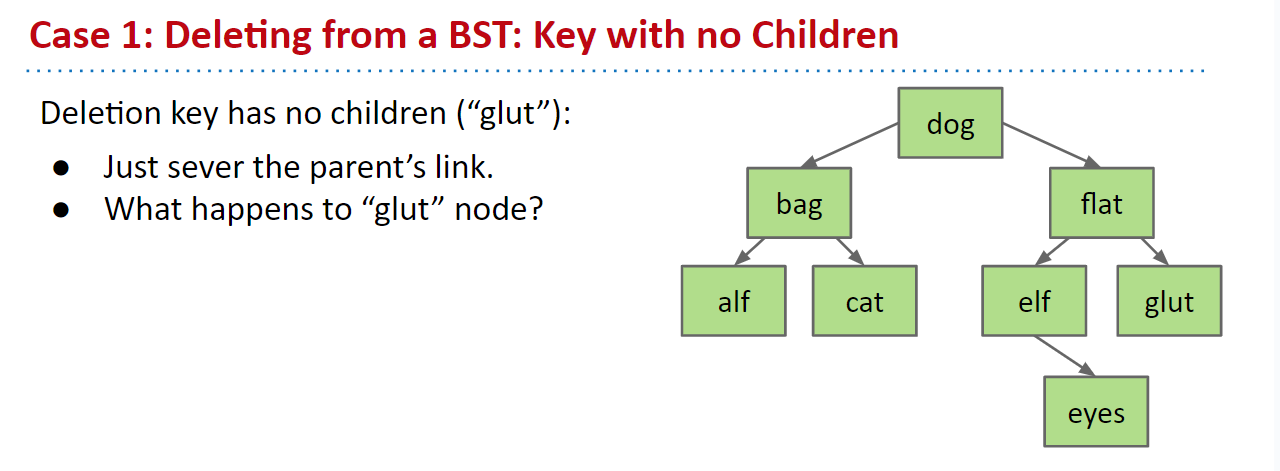
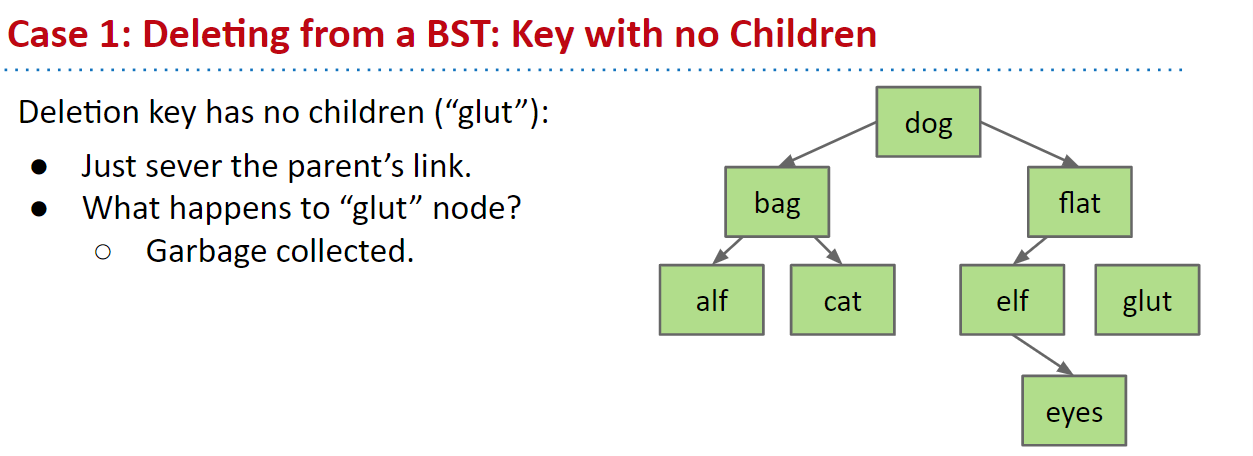
没有子节点
如果节点没有子节点,则它是一个叶子,我们可以只删除其父节点指针,节点最终会被垃圾回收器清除。
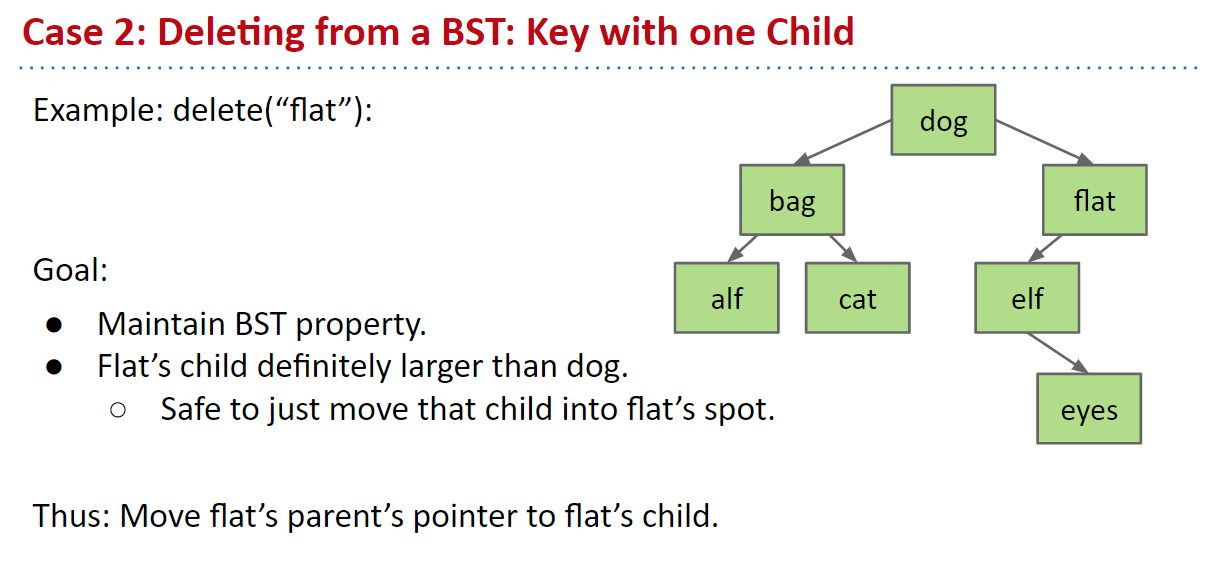
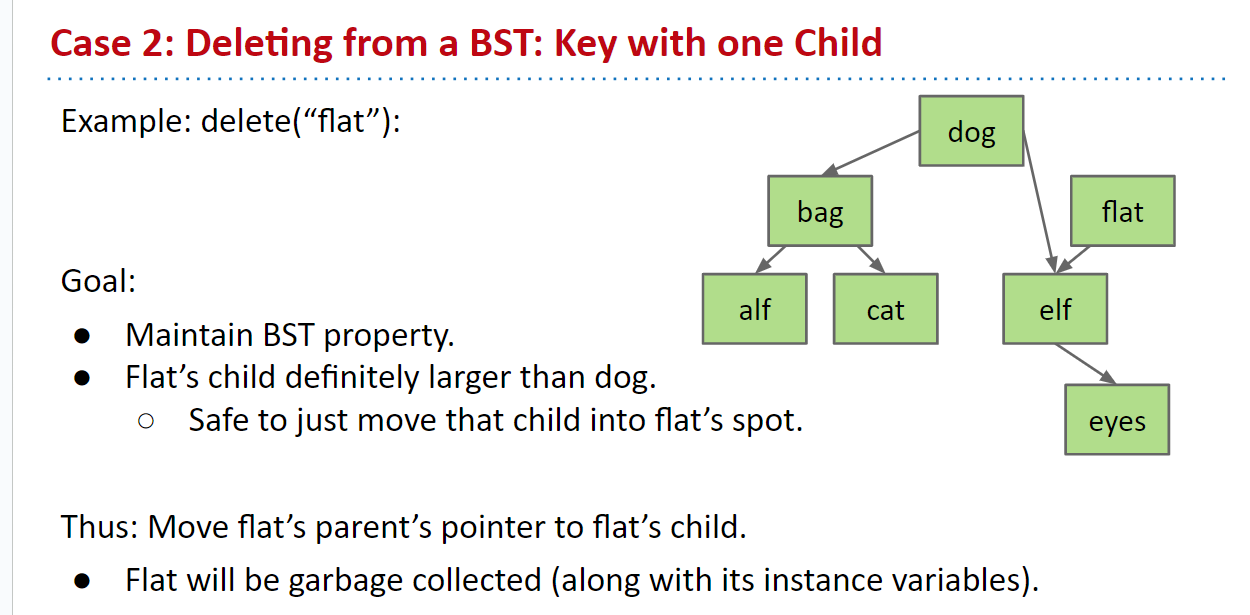
一个子节点
如果节点只有一个子节点,我们知道该子节点与节点的父节点保持BST属性,因为该属性对右和左子树是递归的。因此,我们只需重新分配父节点的子节点指针到节点的子节点,节点最终将被垃圾回收。
两个子节点
如果节点有两个子节点,则该过程变得稍微复杂,因为我们不能简单地将一个子节点指定为新根。这可能会破坏BST属性。
相反,我们选择一个新节点来替换删除的节点。
我们知道新节点必须:
- 大于左子树中的所有内容。
- 小于右子树中的所有内容。
在下面的树中,我们展示了哪些节点将满足这些要求,假设我们要删除dog节点。
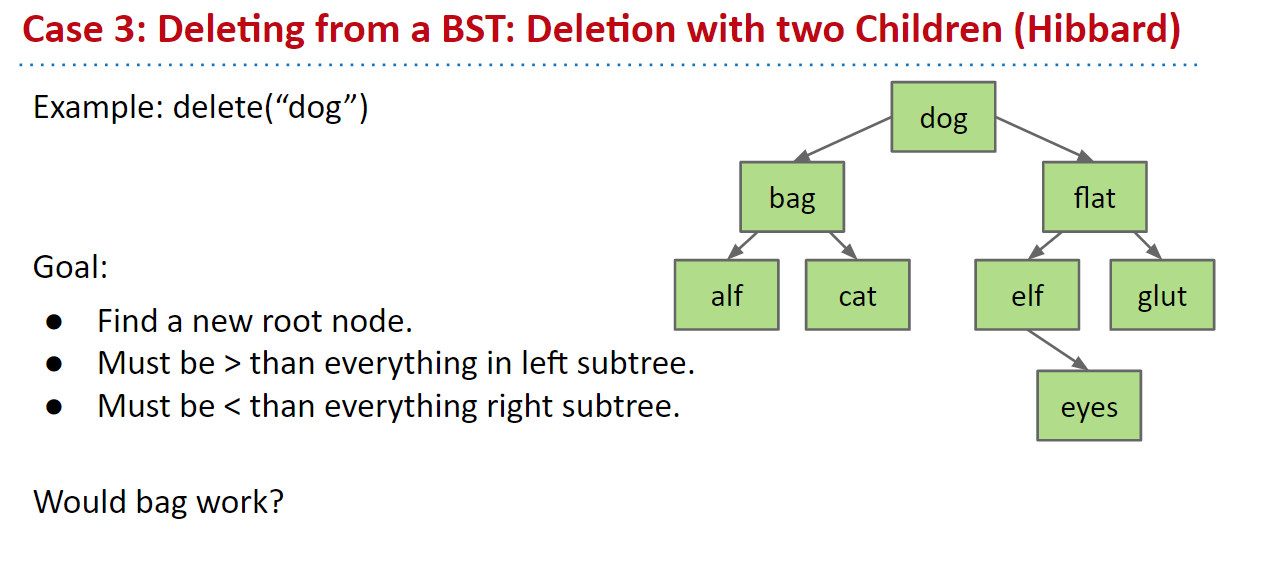
要找到这些节点,您可以选择左子树中的最右节点或右子树中的最左节点。
然后,我们用cat或elf替换dog节点,然后删除旧的cat或elf节点。
这称为Hibbard删除,在删除中保持了BST属性。
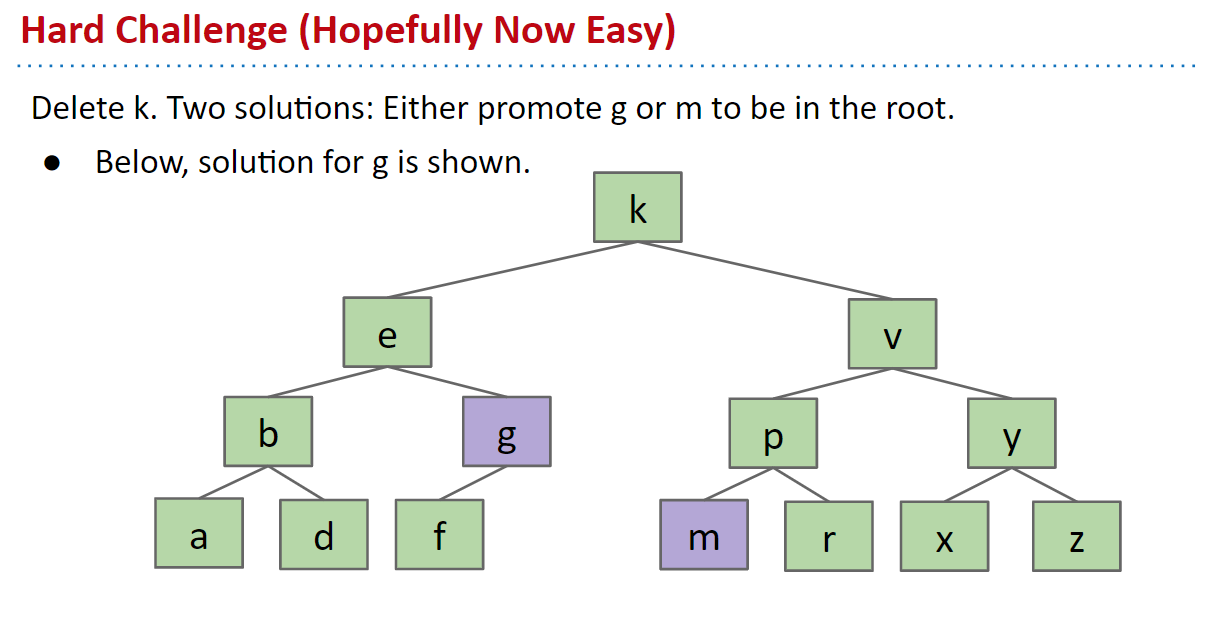
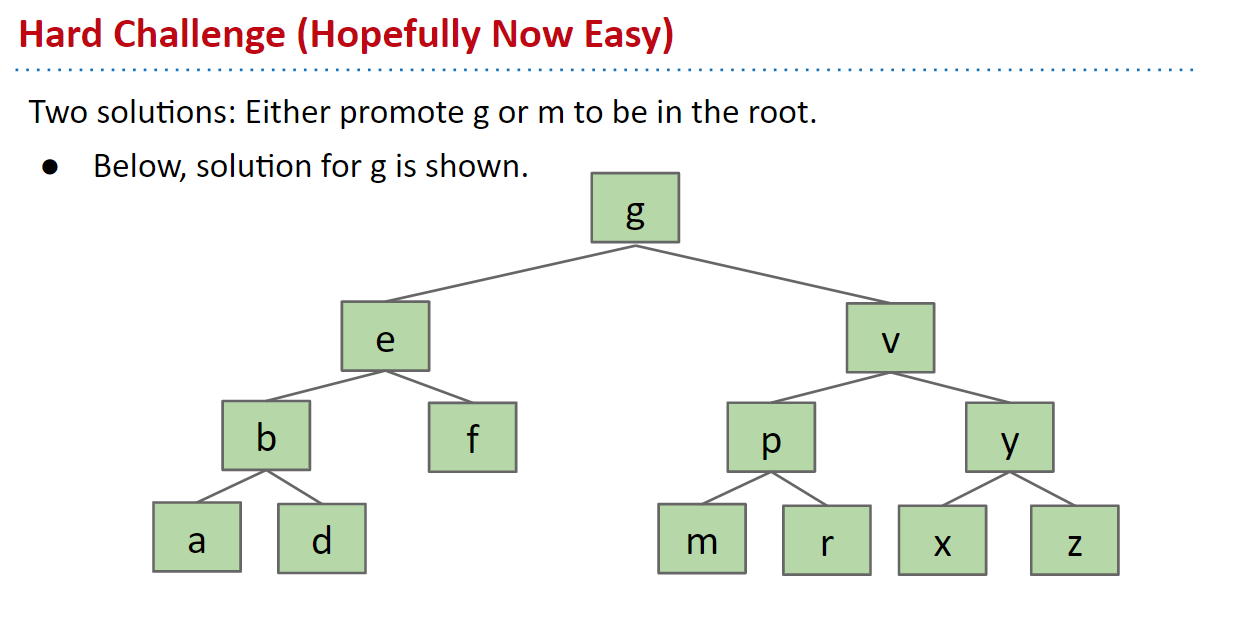
若将树重新拉直,k左右两边将会是g和m,我们只需要将其中一个替换掉k,那么就能实现删除的同时保持树的特性!
作为集合和映射的BST
我们可以使用BST来实现Set ADT!但是它更好,因为在ArraySet中,我们需要在最坏的情况下O*(*n*)时间来运行contains,因为我们需要搜索整个集合。但是,如果我们使用BST,我们可以将此运行时间减少到log(n)`,因为BST属性使我们能够使用二分查找!
我们还可以通过使每个BST节点保存(key,value)对而不是单个值来将二叉树转换为映射。我们将比较每个元素的键以确定在树中的位置。
总结
抽象数据类型(ADTs)是根据操作而不是实现来定义的。
几种有用的ADT:
- 不相交集、映射、集合、列表。
- Java提供了映射、集合、列表接口,以及几种实现。
我们已经看到了实现Set(或Map)的两种方法:
- ArraySet:在最坏的情况下,需要
Θ(*N*)的操作。 - BST:如果树是平衡的,则需要Θ(logN)`的操作。
BST实现:
- 搜索和插入都很简单(但插入有点棘手)。
- 删除更具挑战性。典型的方法是“Hibbard删除”。