CS61B学习笔记(十七)-RD17、18、19-树遍历与图
树的遍历
树的回顾
树的定义
回想一下,一棵树由以下部分组成:
- 一组节点(或顶点)。
- 连接这些节点的一组边。
- 约束:任意两个节点之间只有一条路径。
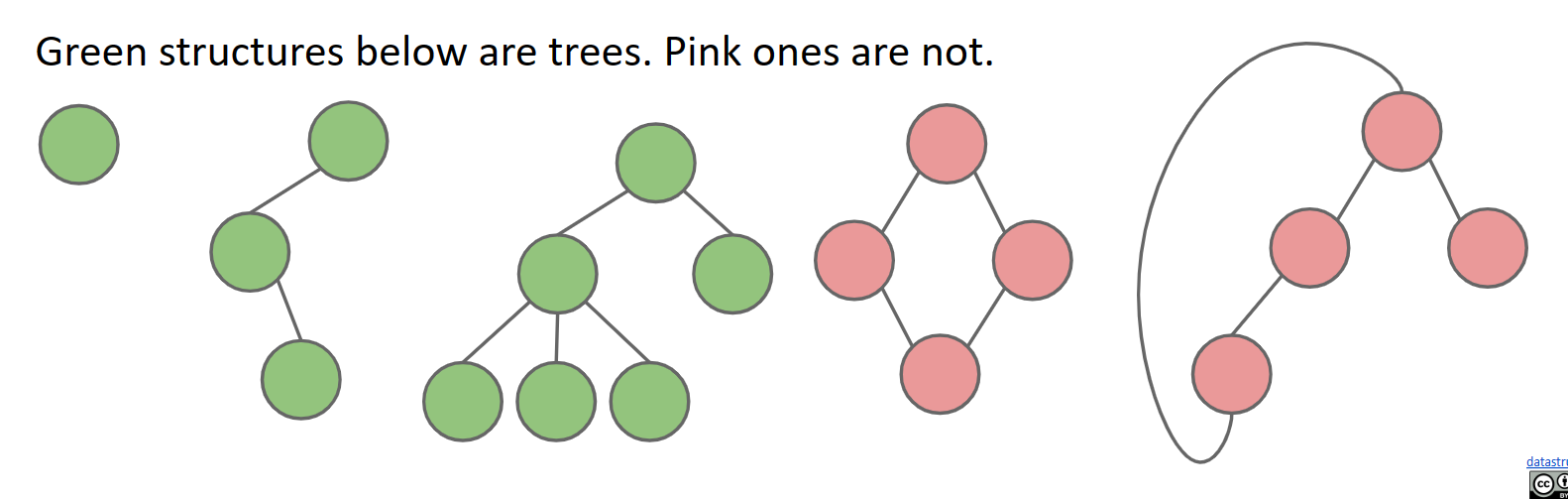
树有什么用?
到目前为止,我们已经了解了搜索树、尝试、堆、不相交集等。这些在我们创建高效算法的过程中非常有用:加快搜索项、允许添加前缀、检查连通性等。
但事实是它们比我们意识到的更加普遍。考虑一个组织结构图。在这里,总统是“根”。 “VP”是根的子代,依此类推。
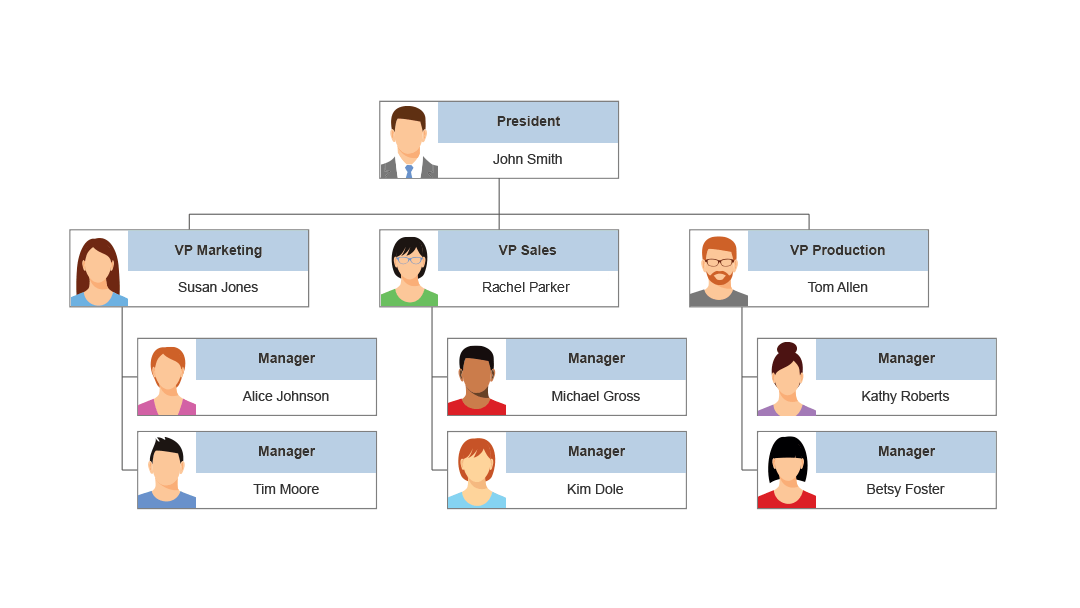
另一个树结构是桌面上的 61b/ 目录(它就在您的桌面上,不是吗?)。正如我们所看到的,当您遍历到子文件夹时,它会转到后续子文件夹,依此类推。这简直就像树一样!
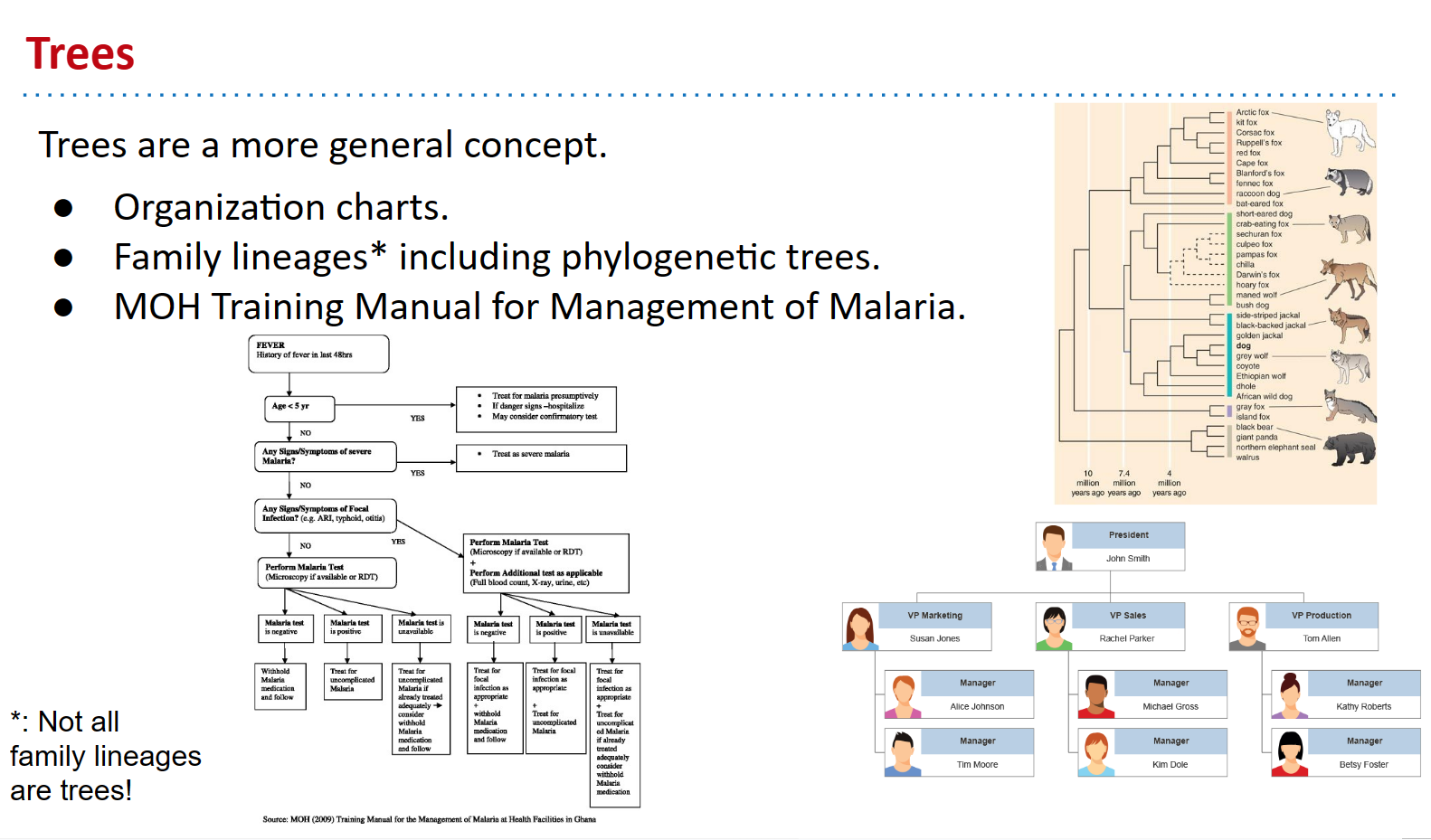
Tree Iteration Traversal
回想一下我们如何学会遍历列表的?有一种遍历列表的方式感觉很自然。就是从开头开始…然后继续往下走。
或者也许我们做了一些有点奇怪的事情,比如遍历列表的反向。回想一下,我们还在讨论中编写了迭代器,以跳过没有在 Office Hours 排队中写描述的学生。
现在如何遍历一棵树呢?什么是正确的“顺序”?
在回答这个问题之前,我们不能使用迭代这个词。相反,我们将称之为“遍历树”或“树遍历”。为什么呢?除了每个人都称通过树进行迭代为“遍历”之外,没有真正的理由。也许是因为世界喜欢头韵。
那么,通过树“遍历”的一些自然方法是什么?事实证明,有一些方法——与列表基本上只有一种自然的迭代方式不同:
- 层次遍历。
- 深度优先遍历——其中有三种:前序、中序和后序。
让我们在下面的树上测试上述遍历方法。
层次遍历
我们将按层次从左到右进行迭代。第 0 层?D。第 1 层?B,然后是 F。第 2 层?A,C,E 和 G。
这给我们 D B F A C E G。
想象每一层都是英语中的一个句子,我们只需逐行阅读它。
练习 17.2.1. 编写执行层次遍历的代码(警告,这比编写其他遍历更难)。提示:您将需要跟踪您所在的层级。
前序遍历
前序遍历的思想很简单。从根开始。访问根(也就是,执行你想要的操作)。这里的操作是“打印”。
所以,我们将打印根。D。就这样。
现在,向左走,然后递归。然后,向右走并递归。
所以现在我们已经向左走了。我们在 B 节点。打印它。B。我们在打印后向左走。(记住,当我们完成了 B 的左分支后,我们会回来访问 B 的右分支。)
继续遵循这个逻辑,你会得到 D B A C F E G。
1 | preOrder(BSTNode x) { |
中序遍历
稍微不同,但大体思路相同。这里,我们首先访问(也就是打印)左分支,然后我们打印。然后我们访问右分支。
所以我们从 D 开始。我们不打印。我们向左走。
我们从 B 开始。我们不打印。我们向左走。
我们从 A 开始。我们不打印。我们向左走。我们什么也没找到。我们回来,打印 A。
然后去 A 的右边。找不到任何东西。返回。现在我们在 B。记住,在访问左边和访问右边之前打印,所以现在我们将打印 B,然后我们将访问右边。
继续遵循这个逻辑,你会得到 A B C D E F G。
另一种思考方法是:
首先,我们在 D。我们知道我们将先打印左边的项目,然后是 D,然后是右边的项目。
[左边的项目] D [右边的项目]。
现在左边的项目等于什么?我们从 B 开始,打印左边,然后打印 B,然后打印 B 的右边的东西。
[左边的项目] = [B 的左边的项目] B [B 的右边的项目] = A B C。
A B C D [右边的东西] = A B C D E F G。
1 | inOrder(BSTNode x) { |
后序遍历
同样的大体思路,但现在我们将打印左分支,然后右分支,然后是自己。
使用我们之前设计的方法,结果如下:
[左边的项目] [右边的项目] D。
左边的项目是什么?它是 B 子树的输出。
如果我们在 B,我们会得到 B 的左边的项目 B 的右边的项目 B,等于 A C B。
按照这个思路,我们得到:A C B E G F D
1 | postOrder(BSTNode x) { |
堆栈思路思考
二叉树遍历方法——前、中、后序遍历(图解)_前序遍历-CSDN博客
图
树很棒,不是吗?但正如我们所看到的,我们可以使用节点和边来绘制一些不是树的东西。具体来说,我们之前的限制,即任何两个节点之间只能有一条路径,不适用于所有情况。让我们看看当我们取消了这个限制会发生什么。
什么是图?
图由以下组成:
- 一组节点(或顶点)
- 一组零个或多个边,每条边连接两个节点。
就是这样!没有其他限制。
下面以绿色显示的所有结构?都是有效的图!第二个也是一棵树,但其他都不是。
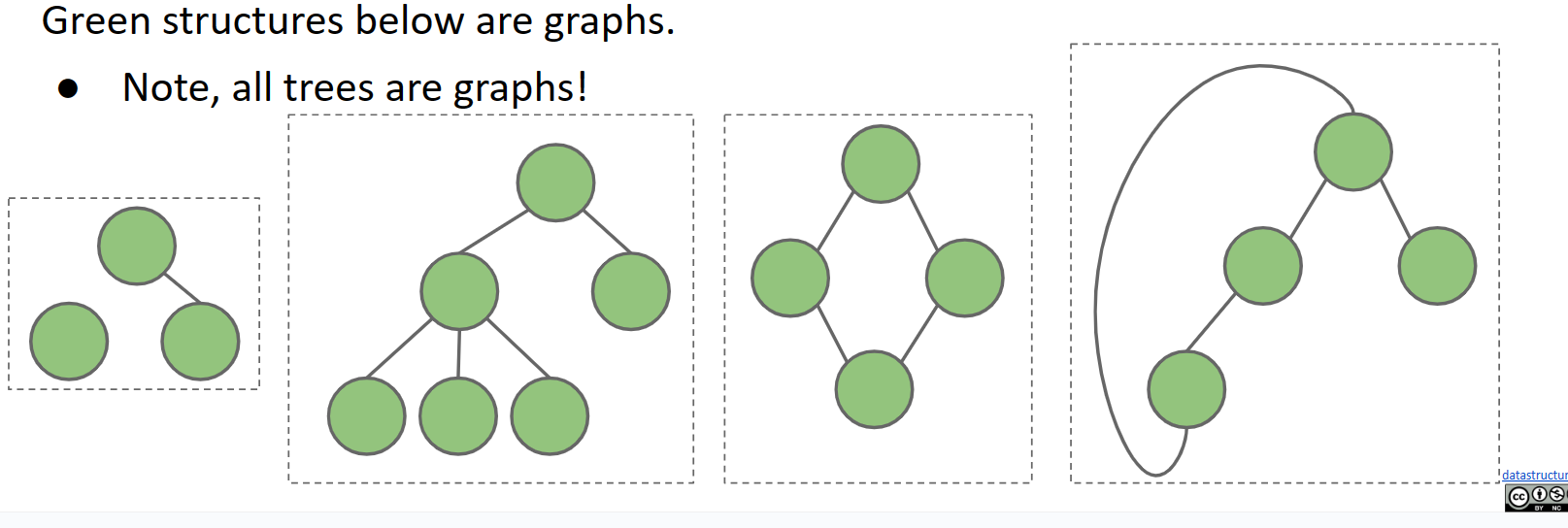
一般来说,需要注意的是所有树也都是图,但并非所有图都是树。
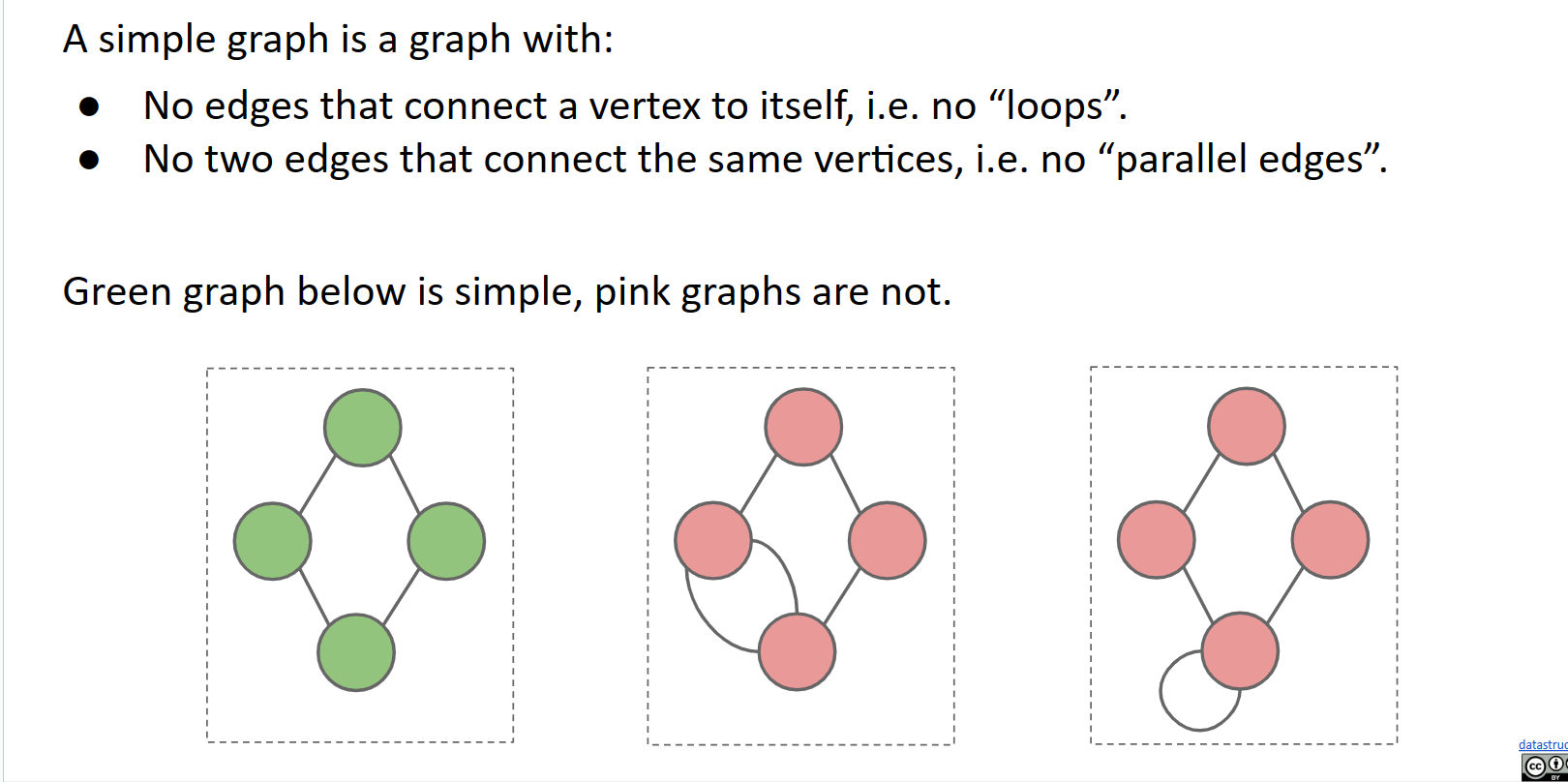
仅有简单图
图可以分为两类:简单图和多重图(或复杂图)。幸运的是,在这门课程中(以及几乎所有的应用和研究中),我们只关注简单图。所以在这门课程中,当我们说“图”时,你应该始终将其视为“简单图”(除非另有说明)。
好了,现在是解决问题的时候了。什么是简单图?
看一下红色的图。中间的图从/到底部的下一个节点和/或从/到底部的左侧节点有2个不同的边。换句话说,两个节点之间存在多条边。这不是一个简单图,除非另有说明,我们将忽略它们的存在。类似这样的图被称为多重图。
再看第三张图。它有一个环!一个从一个节点到自身的边!我们也不允许这种情况。类似这样的图有时被归类为多重图,有时甚至明确禁止自环。
更多分类
除非另有说明,否则以下文本中的图都是简单图。但还有更多的分类。
- 无向图,其中一条边(u,v)可能意味着从节点 u 到节点 v 的边,也可能意味着从节点 v 到节点 u 的边。有向图,其中边(u,v)表示从 u 开始的边,到达 v(反之则不成立,除非还存在边(v,u))。有向图中的边带有箭头。
- 还有无环图。这些是没有任何环的图。然后有环图,即存在一种方法从一个节点开始,沿着一些唯一的边返回到与起始节点相同的节点。
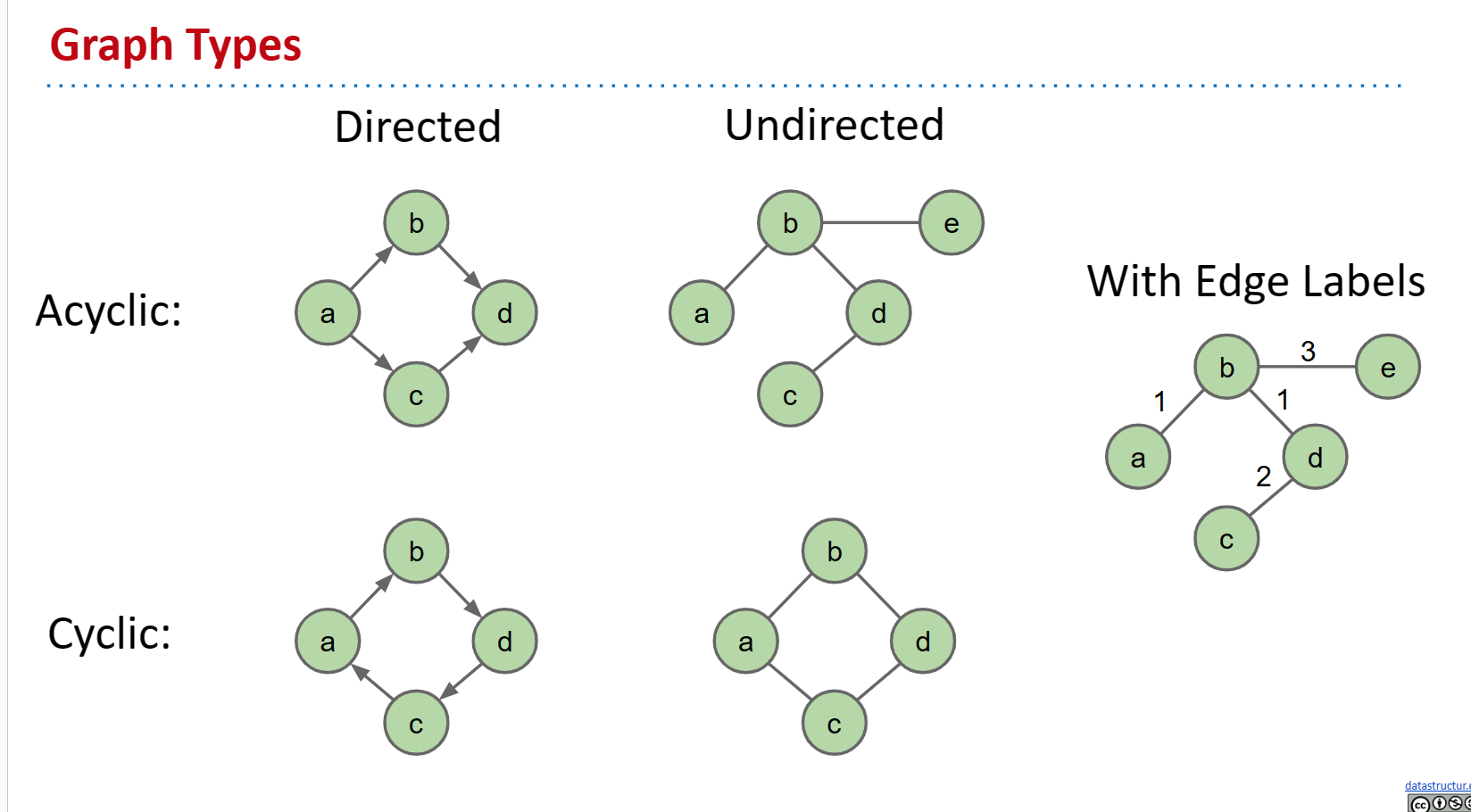
在上面的图片中,我们可以清楚地看到如何绘制有向和无向边之间的差异。
看一下循环图。如果你从 a 开始,你可以沿着仅使用不同边的路径回到 a。因此,该图是有环的。
看一下左上角的图。有没有任何节点 n,如果你从 n 开始,你可以沿着一些不同的边,回到 n?没有!(记住对于有向边,你必须遵循方向。你可以从 a 到 b,但不能从 b 到 a。)
图的遍历
深度搜索(Depth-First Traversal)
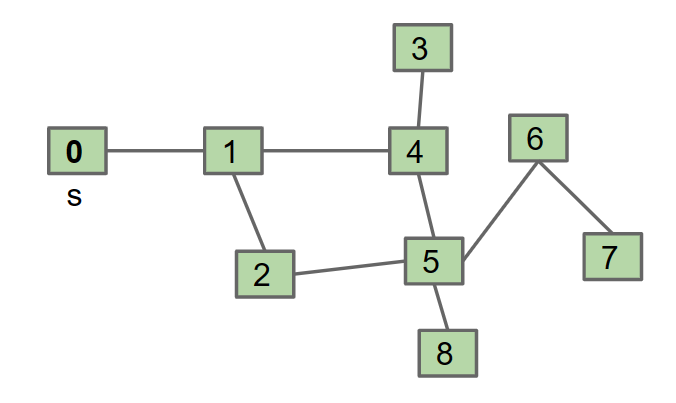
让我们先解决列表中的第一个问题。给定源顶点 s 和目标顶点 t,是否存在两者之间的路径?
换句话说,编写一个名为 connected(s, t) 的函数,该函数接受两个顶点,并返回两者之间是否存在路径。
首先,让我们假设我们有以下代码:
1 | if (s == t): |
但是这个存在一个问题:
我们从 connected(0, 7) 开始, 这将递归调用 connected(1, 7),然后 connected(0, 7)。无限循环发生了。
为了解决这个问题,我们需要标记已经递归过的
1 | mark s // 记住你已经访问过 s 了 |
我们标记了自己。然后我们访问了我们的第一个子节点。然后我们的第一个子节点标记了自己,并访问了它的子节点。然后我们的第一个子节点的第一个子节点标记了自己,并访问了它的子节点。
直观地说,我们会深入(即,沿着我们的家族树向下走到我们的第一个子节点,我们的第一个子节点的第一个子节点,也就是我们的第一个孙子,我们的第一个孙子的第一个子节点,依此类推……访问整个谱系),然后再去触摸我们的第二个孩子。
树遍历和深搜的对比
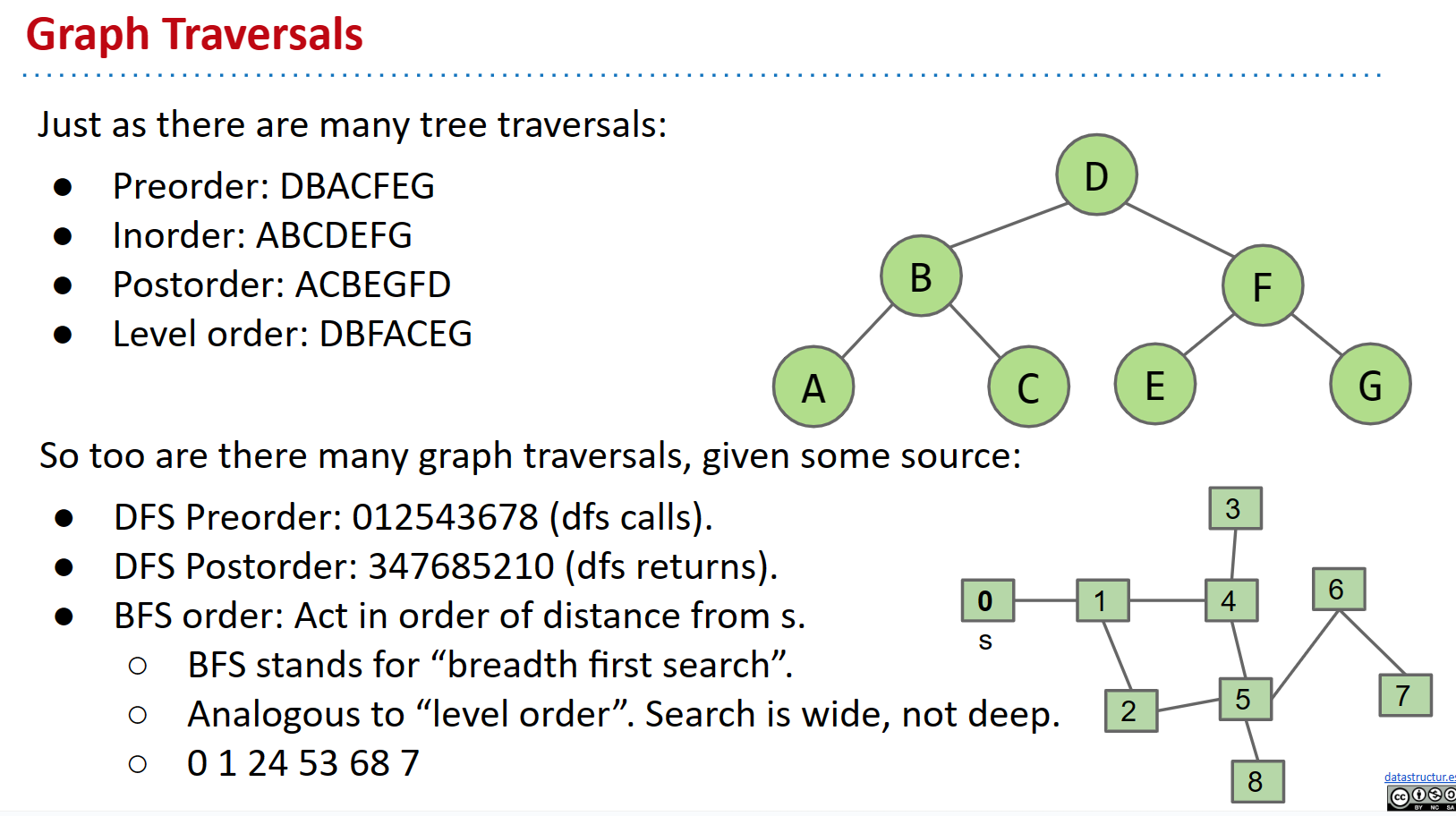
广度优先搜索(Breadth First Search)
也称为层序遍历
在 BFS 中,我们会先拜访所有的直系子女,然后再继续拜访我们的任何孙辈。换句话说,我们访问距源 1 个边的所有节点。然后,所有节点距我们的源有 2 个边,等等。
BFS的伪代码如下:
1 | Initialize the fringe (a queue with the starting vertex) and mark that vertex. |
fringe只是我们用于存储遍历发现过程边界上的节点(它正在等待查看的下一个节点)的数据结构的术语。对于 BFS,我们使用队列作为fringe。
edgeTo[...] 是一个map,可以帮助我们跟踪如何到达节点 n ;我们沿着从 v 到 n 的边缘到达了它。
distTo[...] 是一个map,可以帮助我们跟踪 n 距起始顶点的距离。假设每条边的距离为 1 ,那么到 n 的距离仅比到 v 的距离多一。为什么?我们可以使用我们知道如何到达 v 的方式,然后再支付一次费用,通过 v 和 n (它必须存在,因为在 for 循环头中, n 被定义为 v 的邻居)。
深搜与广搜对比
需要注意的是,深度优先搜索(DFS)和广度优先搜索(BFS)不仅在它们的 fringe 数据结构上有所不同,它们在标记节点的顺序上也有所不同。对于DFS,我们只有在访问到一个节点时才标记它 - 也就是说,从 fringe 中弹出它。因此,如果某个节点已经被添加到队列中但尚未被访问,那么在栈上同时存在多个相同节点的实例是可能的。而对于BFS,我们在将节点添加到 fringe 时立即标记节点,因此不可能出现这种情况。
在DFS中,当遍历到一个节点时,首先将其标记为已访问,然后探索该节点的所有相邻节点。这意味着节点只有在被访问到并从遍历队列中弹出时才被标记。因此,在DFS中,如果一个节点已经被加入到遍历队列中但尚未被访问到,那么它可以被多次加入到栈中,形成多个实例。
相比之下,在BFS中,当一个节点被加入到遍历队列中时,立即将其标记为已访问。这样就不会出现同一节点的多个实例同时存在于队列中的情况,因为每个节点在被添加到队列时就已经被标记过了。
这种不同的节点标记方式导致DFS和BFS在搜索顺序和空间复杂度方面表现出不同的特点。DFS更加深入地搜索图的分支,可能会沿着一条路径一直向下搜索,而BFS则更加广泛地搜索图的各个分支,逐层向外扩展。
递归 DFS 通过递归堆栈帧自然地实现了这一点;迭代DFS手动实现它:
1 | Initialize the fringe, an empty stack |
图的表示
现在让我们花点时间来讨论如何在代码中实现这些图和图算法。
我们将讨论我们的 API 选择,以及用于表示图的底层数据结构。我们的决定可能会对我们的运行时、内存使用情况以及实现各种图算法的难度产生深远的影响。
图 API
API(应用程序编程接口)是我们类的用户可以使用的方法列表,包括方法签名(每个函数接受的参数/参数是什么)以及有关它们行为的信息。你已经见过来自Java开发者的API,比如他们提供的类,比如 Deque。
对于我们的图 API,让我们使用将每个唯一节点分配给一个整数编号的常见约定。这可以通过维护一个映射来实现,该映射可以告诉我们每个原始节点标签分配的整数。这样做可以让我们定义我们的 API 专门与整数一起工作,而不是引入对泛型类型的需求。
然后,我们可以定义我们的 API 看起来可能是这样的:
1 | public class Graph { |
客户端(希望使用我们的图数据结构的人)可以使用我们提供的任何函数来实现自己的算法。我们提供的方法可能会对我们的客户实现特定算法的难易程度产生重大影响。
图的表示
接下来,我们将讨论可以用于表示我们的图的底层数据结构。
邻接矩阵
一种方法是使用二维数组。当且仅当对应的单元格为 1 时(表示为 true),存在从顶点 s 到 t 的边。注意,如果图是无向的,则邻接矩阵将在其对角线上对称(从左上角到右下角的对角线)。
边集
另一种方法是存储所有边的单个集合。
邻接表
第三种方法是维护一个由顶点编号索引的列表数组。当且仅当从 s 到 t 存在一条边时,数组索引为 s 的列表将包含 t。
实际上,邻接表是最常见的,因为图往往是稀疏的(每个桶中没有太多的边)。
效率
您选择的底层数据结构可以影响图的运行时和内存使用情况。幻灯片中的这张表总结了每种表示形式对各种操作的效率。在将此内容复制到您的备忘单上之前,请先花时间了解这些边界是从何而来的。讲座包含了解释其中几个单元格背后原理的步骤。
此外,基于邻接表的图上的DFS/BFS的运行时间为
O(V+E),而基于邻接矩阵的图上的运行时间为
)。请参考幻灯片以帮助理解为什么。



