最短路径(SPT)

回顾

到目前为止，我们有以下方法可以完成以下任务：

  • 找到从给定顶点 s 到图中每个可到达顶点的路径。
  • 找到从给定顶点 s 到图中每个可到达顶点的最短路径。（…或者我们找到了吗？）

在我们回答上述神秘问题之前，让我们进一步回顾一下我们可以使用的两种搜索类型：BFS 或 DFS。

两者都始终正确吗？是的。哪一个结果更好？BFS找到了最短路径，而DFS则没有。在运行时间上，哪一个更有效率？都不是。在空间上，哪一个更有效率？

  • 对于稀疏图，DFS更糟糕。想象一下一个有10000个节点且都很稀疏的图。我们最终会进行10000次递归调用，这对空间来说是不好的。
  • 对于“树状”图，BFS更糟糕，因为我们的队列会经常被使用。

回答神秘问题

我们是否开发了一种算法来找到从给定顶点到每个其他可到达顶点的最短路径？嗯，有点像是。我们开发了一种在没有边标签的图上运行良好的算法。这是我们做的：我们开发了一种算法，它从给定的源顶点找到了我们最短（其中最短的意思是最少的边数）的路径。

但这并不总是最短的正确定义。有时，我们的图边可能有‘权重’，如果 A-B 边的权重为5，而 A-C 边的权重只有3，那么A-B 被认为比 A-C 更远。

考虑以下图像以了解问题所在。

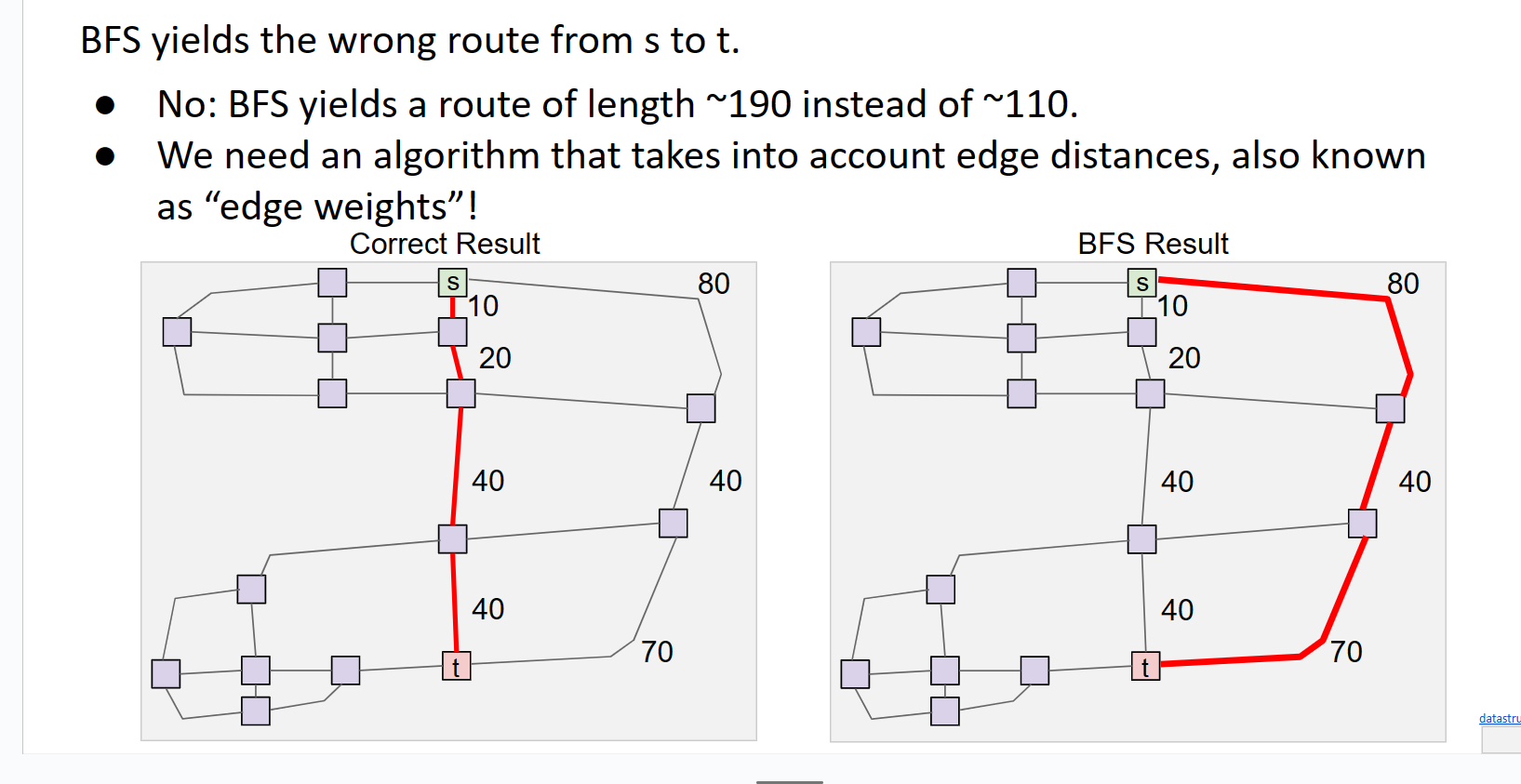
image-20240319234957049

右边边最少但是他并不是最短的

Dijkstra算法

执行以下两项操作。

  1. 查找从标记 0 的顶点到标记的 5 顶点的路径。
  2. 从标记为 0 的顶点中查找最短路径树。（即，找到从图中 0 到每个顶点的最短路径。
  3. 尝试想出一种算法来做到这一点。

观察

注意最短路径（对于带有权重的图）可能有许多许多边。我们关心的是选择路径上边的权重之和的最小化。

其次，请注意从源s到达的最短路径树可以通过以下方式创建：

  • 对于图中的每个顶点v（不是s），找到从s到v的最短路径。
  • “合并”所有上述找到的边。完成！

第三，请注意“最短路径树”将始终是一棵树。为什么？嗯，让我们考虑一下我们的原始解决方案，其中我们维护了一个edgeTo数组。对于每个节点，在edgeTo数组中恰好有一个“父节点”。（这为什么意味着“最短路径树”将是一棵树？提示：一棵树有V-1条边，其中V是树中的节点数。）

Dijkstra算法接受输入顶点s，并输出从s出发的最短路径树。它是如何工作的呢？

  1. 创建一个优先队列。
  2. 将s添加到优先队列，并将优先级设置为0。将所有其他顶点添加到优先队列，并将优先级设置为∞。
  3. 当优先队列不为空时：弹出优先队列中的一个顶点，并释放该顶点出发的所有边。

什么是释放？

假设我们刚刚从优先队列中弹出的顶点是v。我们将查看v的所有边。假设我们正在查看边(v,w)（从v到w的边）。我们将尝试对这条边进行释放。

这意味着：查看您从源到w的当前最佳距离，称为curBestDistToW。现在，查看curBestDistToV+weight(v, w)（称为potentialDistToWUsingV）。

potentialDistToWUsingV是否更好，即更小，比curBestDistToW？在这种情况下，将curBestDistToW=potentialDistToWUsingV，更新edgeTo[w]为v。

重要说明：我们不会释放指向已访问顶点的边。

计算潜在距离、检查是否更好以及可能更新的整个过程称为释放。

通过以下图像捕获了另一种定义。img

伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def dijkstras(source):
    PQ.add(source, 0)
    For all other vertices, v, PQ.add(v, infinity)
    while PQ is not empty:
        p = PQ.removeSmallest()
        relax(all edges from p)
def relax(edge p,q):
   if q is visited (i.e., q is not in PQ):
       return

   if distTo[p] + weight(edge) < distTo[q]:
       distTo[q] = distTo[p] + w
       edgeTo[q] = p
       PQ.changePriority(q, distTo[q])

保证

只要边都是非负的，迪杰斯特拉算法就保证是最优的。

证明和直觉

假设所有边都是非负的。

  • 在开始时，distTo[source] = 0。这是最优的。

  • 在从源开始释放所有边之后，让顶点v1是权重最小的顶点（即距离源最近的顶点）。

    声明：distTo[v1]是最优的，即在此时刻，distTo[v1]的值是从s到v1的最短距离。为什么？

    • 让我们尝试理解为什么必须如此。
    • 假设不是这种情况。那意味着从s到v1存在一条比直接路径(s,v1)更短的路径。好的，那么让我们考虑这条假设中更短的路径…它将会是(s,va,vb,…,v1)这样的路径。但是…(s,va)已经比(s,v1)大了。（请注意，这是因为v1是上面最接近s的顶点。）那么如何可能存在一条实际上更短的路径呢？不可能！

  • 现在，下一个弹出的顶点将是v1。（为什么？请注意，它目前在优先队列中的优先级最低！）

  • 所以现在，我们可以为v1及其进行的所有释放做出同样的论证。（这称为“归纳证明”。这有点像证明的递归。）就是这样；我们完成了。

负边？

当负边出现时，情况可能会变得非常糟糕。考虑以下图像。

假设您在标记为34的顶点。现在，您将尝试释放所有您的边。您只有一条从自己到标记为33的顶点的出边，权重为−67。啊，但是请注意：顶点33已经被访问（用白色标记）。所以…我们不会对其进行释放。（回顾一下relax方法的伪代码。）

现在我们回家，认为到33的最短距离是82（用粉色标记）。但实际上，我们应该走通过34的路径，因为这会给我们34−67=34的距离。糟糕。

对于负边，Dijkstra算法不能保证正确。它可能有效…但不能保证有效。

试一试：假设您的图具有负边，但所有负边都只从您传入的源顶点s出发。迪杰斯特拉算法有效吗？为什么/为什么不？

一个值得注意的不变性

请注意，一旦顶点从优先队列中弹出，它就永远不会被重新添加。它的距离永远不会被更新。因此，换句话说，一旦顶点从优先队列中弹出，我们知道到该顶点的真正最短距离。

这个事实的一个好处是“短路”。假设…我不关心最短路径树，而只想找到从某个源到某个其他目标的最短路径。假设您想要在世界各城市上构建一个图，并找到从伯克利到奥克兰的最短路径。运行dijkstra(Berkeley)将意味着您无法停止这个强大的算法…您必须让它运行…直到它找到到洛杉矶、休斯顿、纽约市和所有可能的地方的最短路径！

好吧。一旦算法中的Oakland从优先队列中弹出，我们就可以停止。我们只需返回此时的距离和路径，它将是正确的。因此，有时dijkstra不仅接受源，还接受目标。这是为了短路的目的。

A*算法

我们通过讨论一种可能的方法来结束Dijkstra算法部分，即使其在碰到给定目标后就停止。这样做足够好吗？

要回答上面的问题，我们需要坐下来思考Dijkstra算法的实际工作原理。以图形方式表示，Dijkstra从源节点开始（想象源节点是圆心）。然后，Dijkstra算法围绕这一点以递增的半径绘制同心圆，并“扫描”这些圆，捕捉点。

因此…Dijkstra首先访问的节点是距离源点最近的城市，然后是次最近的城市，依此类推。这听起来是个好主意。Dijkstra首先访问距离1个单位的所有城市，然后是距离2个单位的城市，依此类推，形成同心圆。

现在想象一下以下情况：在美国地图上，从中心某处开始，比如丹佛。现在我想让你用Dijkstra找到一条到纽约的路径。你将按照“最接近的同心圆”的顺序遍历节点。

你将首先绘制一个小圆，就在丹佛附近，访问该圆内的所有城市。最终，你的圆将变大，你将绘制一个通过拉斯维加斯的圆（到目前为止，该圆将访问所有其他位于圆内的城市）。然后，你的圆将足够大，能够覆盖洛杉矶和达拉斯…但你离纽约还差得远。所有这些努力，所有这些圆，但是…离目标还很远。短路帮助了，但只有在你快速到达目标节点时才有效。

如果我们能有一种方法利用你的先验知识：纽约在东边，这样你就可以“提示”你的算法更喜欢东边的节点，而不是西边的节点。

引入：A*

不，不是太阳。这是一种叫做A*的算法。

观察以下事实：Dijkstra是从源到节点的距离的“真实”（即不是估计）度量。因此，假设你访问了伊利诺伊州的一个城市，你的源是丹佛，那么在那时，你已经得到了到丹佛的距离的真实度量。我们缺少的是：从节点到目标节点纽约的距离的一些粗略估计。这将完整地呈现出整个图景。因为如果你把这两个因素相加（从源到节点的度量+从节点到目标的估计），你得到（从源到目标的估计）。当然，你原始的从节点到目标的估计越好，你从源到目标的估计就越好，你的A*算法就越好。

因此，让我们稍微修改我们的Dijkstra算法。在Dijkstra中，我们使用bestKnownDistToV作为我们算法中的优先级。这次，我们将使用bestKnownDistToV+estimateFromVToGoal作为我们的启发式。

这里有一个演示！

鸡和蛋

我们有一个问题。我们怎么知道估计值是多少？我的意思是，估计值本身是一种距离，而我们正在使用A*来找到从某个节点到另一个节点的距离。

这似乎像是一个经典的鸡和蛋问题实例。“先有鸡还是先有蛋？”顺便说一下，有个Reddit用户对此有了一个想法。

嗯，它被称为估计，因为它确实是这样。我们使用A*来得到从源到目标的真实最短路径，但估计值是我们近似的。有时候得到好的估计是困难的。

但是，让我们以丹佛 - 纽约的例子来举例说明。我们可以做的是查找这些城市的GPS坐标，并计算其中的直线距离。当然，这可能不正确，因为从丹佛到纽约可能没有直线可走，但这是一个相当好的估计！

不好的启发式

假设从丹佛到纽约的最短路径经过某个城市C。假设我的GPS坏了，因此我认为这个城市C离一切都是无限远的，所以我将从图中的每个其他节点到城市C的估计距离设置为∞。

会发生什么？嗯，A*基本上永远不想访问这个城市。 （记住我们在优先级队列中的优先级是什么；对于这个城市，优先级将始终为∞，即使

最小生成树(MST)

最小生成树（MST）是图中可能的最轻的边集，使得所有顶点都连接在一起。由于它是一棵树，它必须是连通的且无环的。而且它被称为“生成”，因为所有顶点都包括在内。

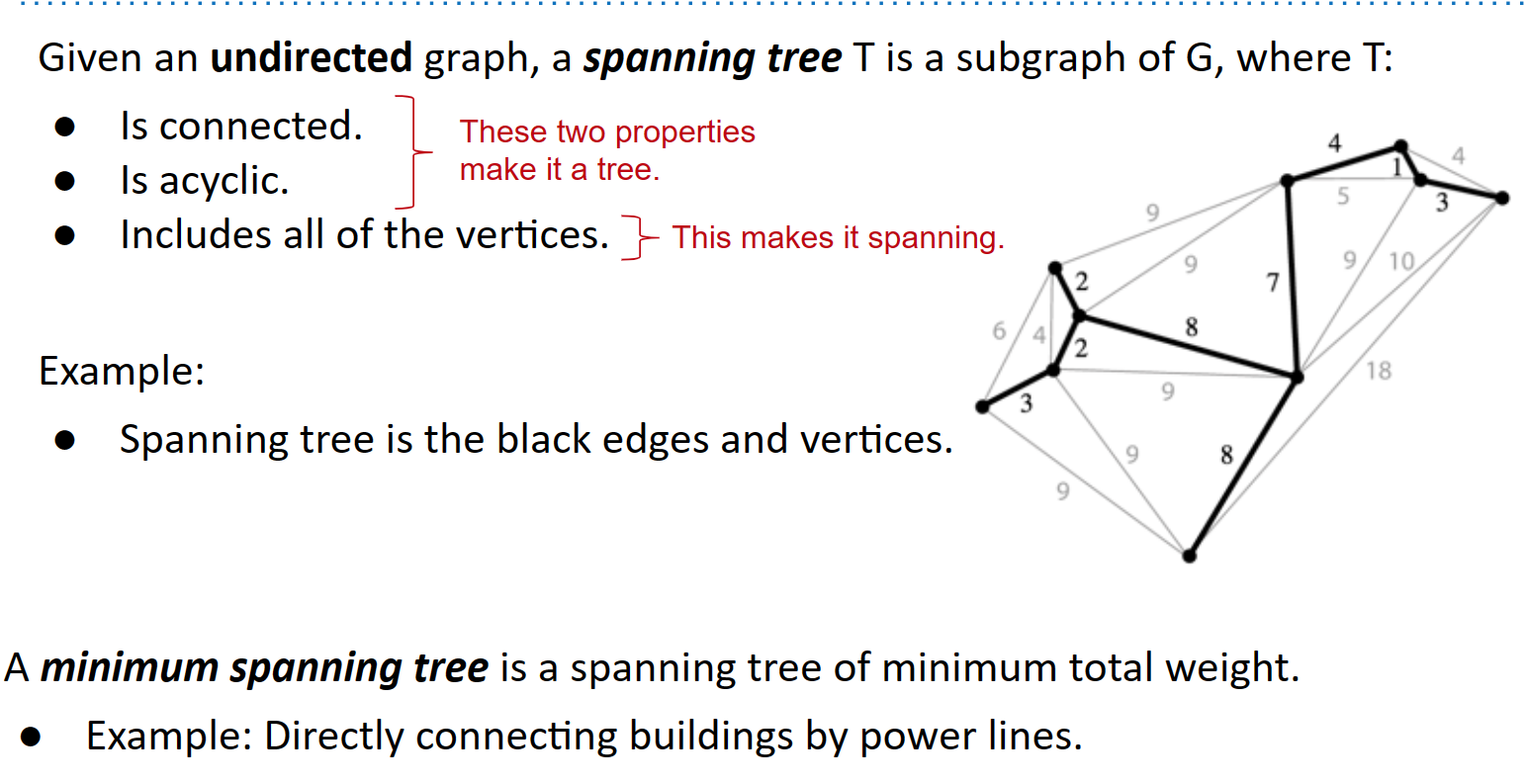
image-20240320172133841

  • 条件

    • 连接的

    • 非闭环的

    • 包括了所有顶点

在这一章中，我们将看两个算法，它们将帮助我们从一个图中找到一个最小生成树。

在我们开始之前，让我们介绍一下割属性，这是一个有助于找到最小生成树的工具。

割属性

我们可以将一个割定义为对图的节点分配给两个非空集合（即我们将每个节点分配给第一个集合或第二个集合）。

我们可以将一个横跨的边定义为连接一个集合中的节点到另一个集合中的节点的边。

有了这两个定义，我们就可以理解割属性了：给定任何一个割，最小权重的横跨边都在最小生成树中。

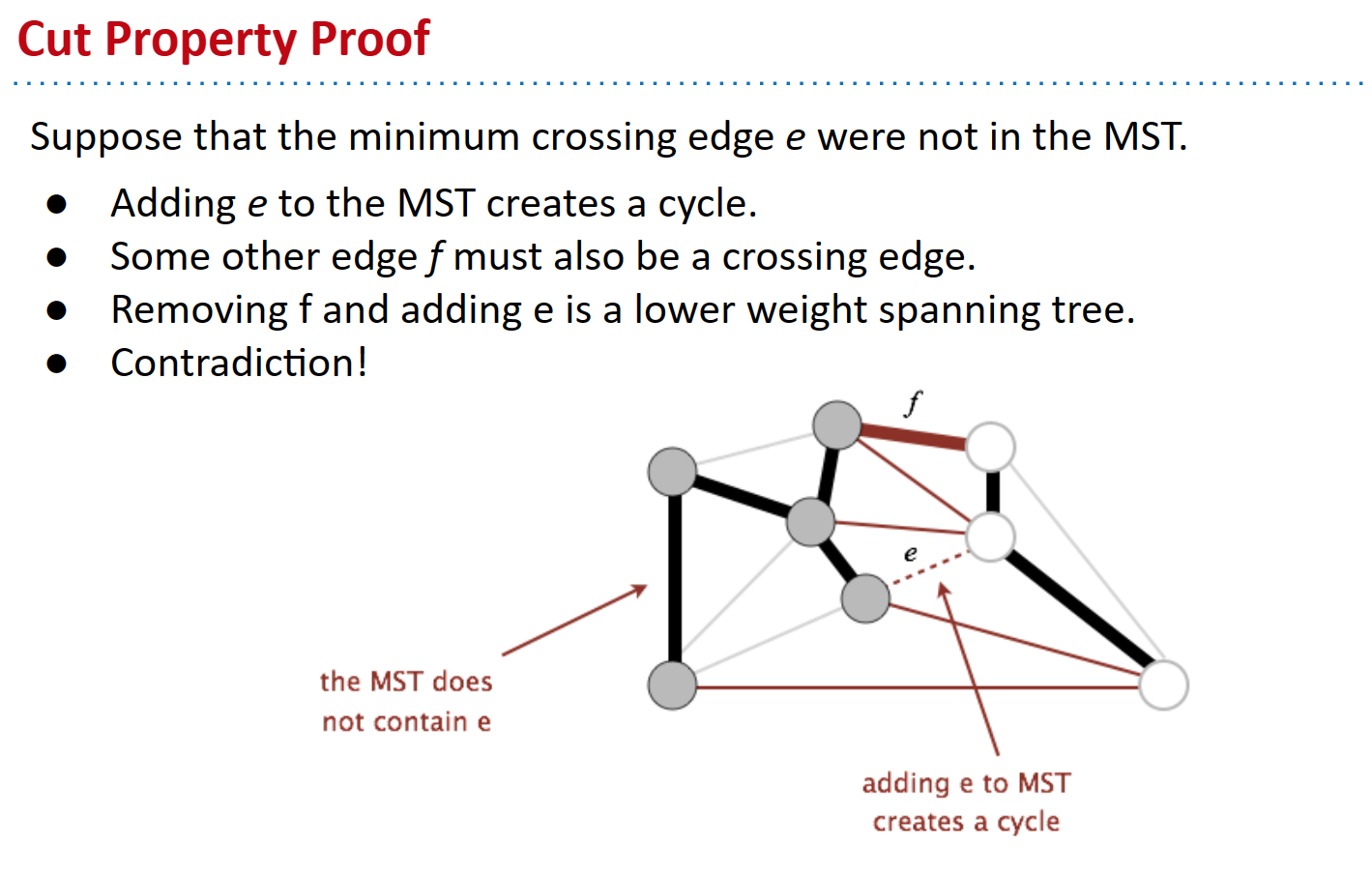
割属性的证明如下：假设（为了推导矛盾）最小横跨边 e 不在最小生成树中。由于它不是最小生成树的一部分，如果我们添加该边，就会创建一个循环。因为有一个循环，这意味着另一个边 f 也必须是一个横跨边（对于一个循环，如果 e 从一个集合穿过到另一个集合，就必须有另一条边穿过回到第一个集合）。因此，我们可以移除 f 并保留 e，这将给我们一个更低权重的生成树。但这是一个矛盾，因为我们假设开始时有一个最小生成树，但现在我们有了一个权重更小的生成树，因此原始的最小生成树实际上并不是最小的。因此，割属性必须成立。

下面是一张图示，说明了上述证明的一些论点：

image-20240320172407081

Prim算法

这是一种从图中找到最小生成树（MST）的算法。它的步骤如下：

  1. 从任意起始节点开始。
  2. 反复添加具有一个节点在正在构建的MST内的最短边。
  3. 重复直到有$V-1$条边。

Prim算法之所以有效，是因为在算法的所有阶段，如果我们将所有节点都作为我们正在构建的MST的一部分，而将所有其他节点视为第二个集合，那么这个算法总是添加横跨此割的最轻的边，根据割属性，这个边必然是最终MST的一部分。

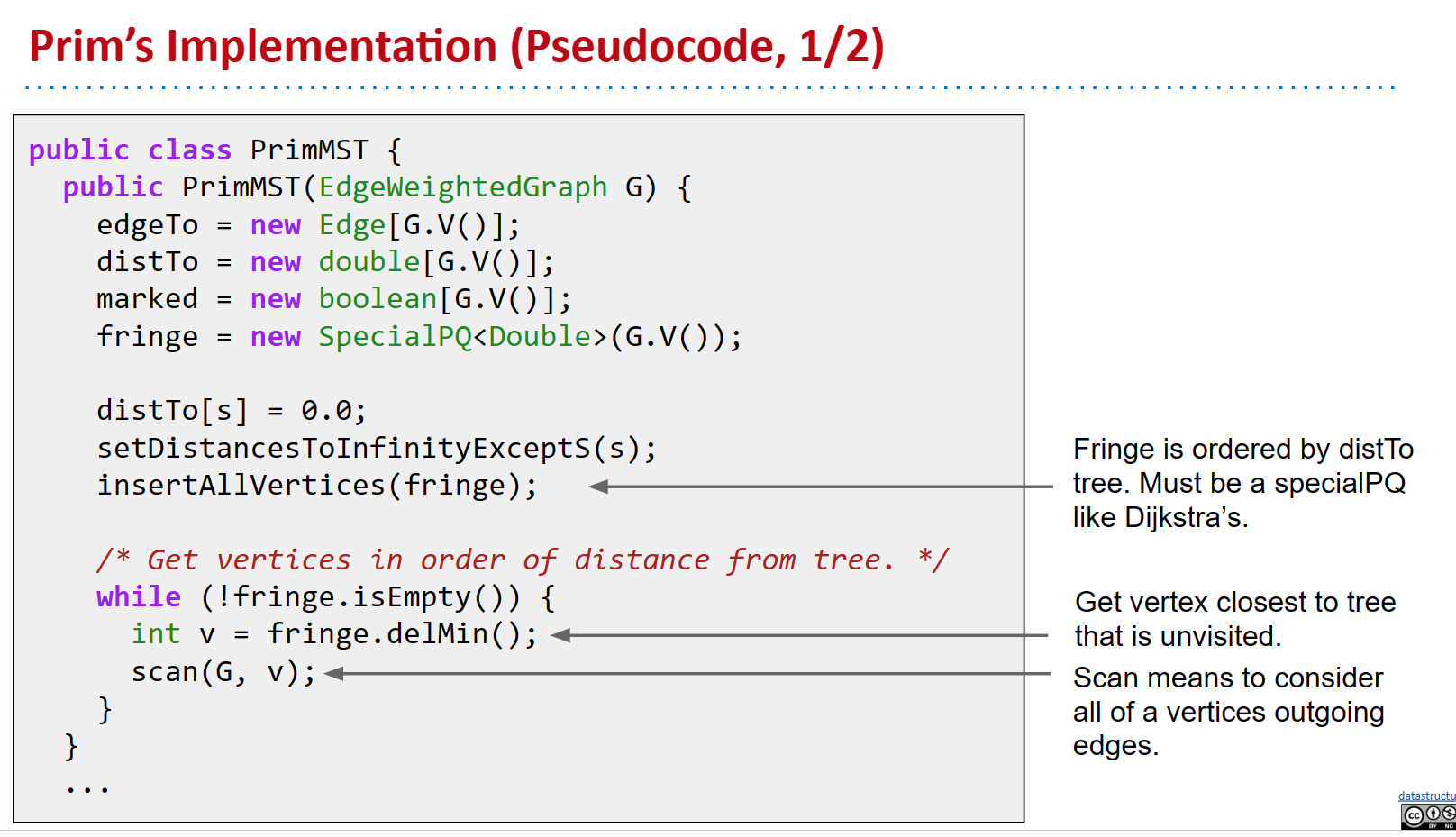
从本质上讲，该算法通过与Dijkstra算法相同的机制运行，但是Dijkstra算法考虑的是候选节点距离源节点的距离，而Prim算法则查看每个候选节点距离正在构建的MST的距离。

因此，如果使用与Dijkstra算法相同的机制进行Prim算法，其运行时间将与Dijkstra算法相同，即

$O((|V| + |E|) \log |V|)$。请记住，这是因为我们需要为每条边添加到优先级队列中的外围，并且我们需要为每个顶点从中出队一次。

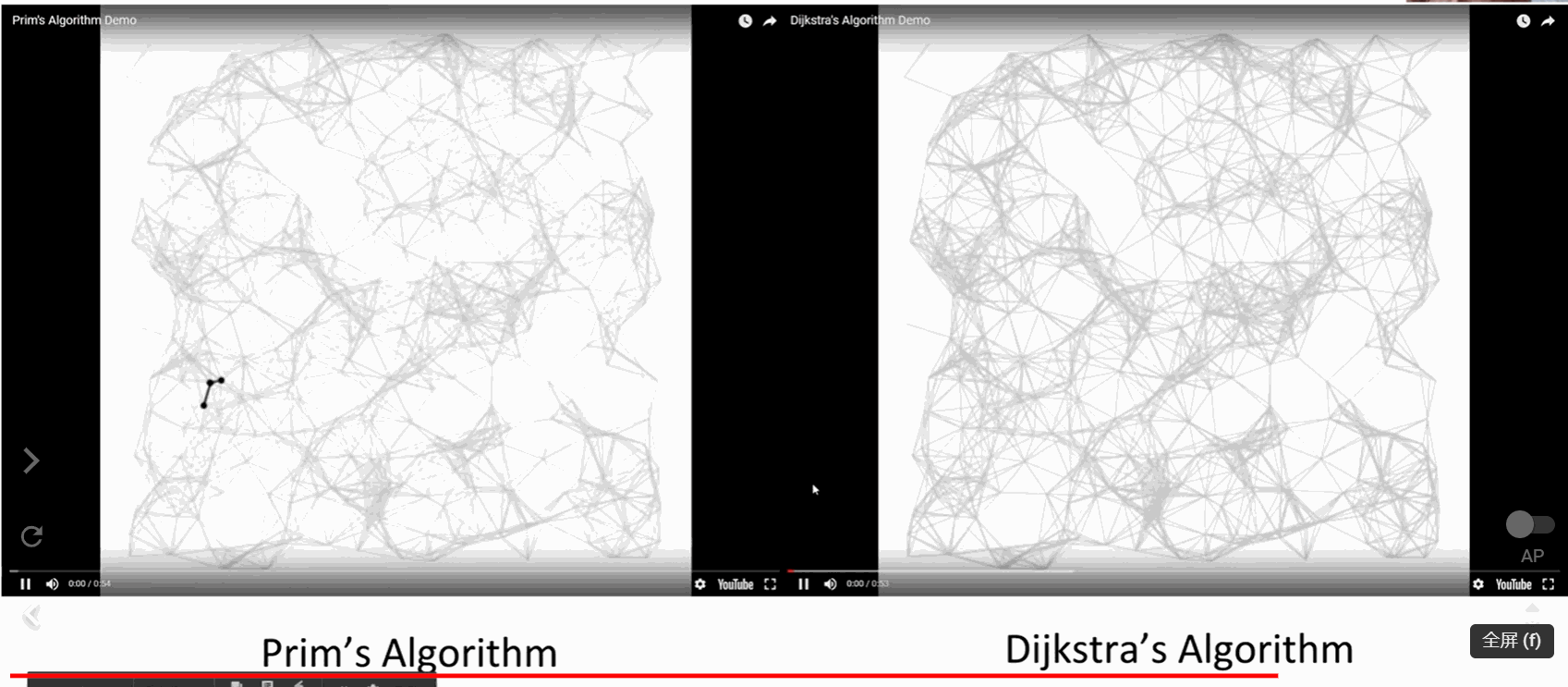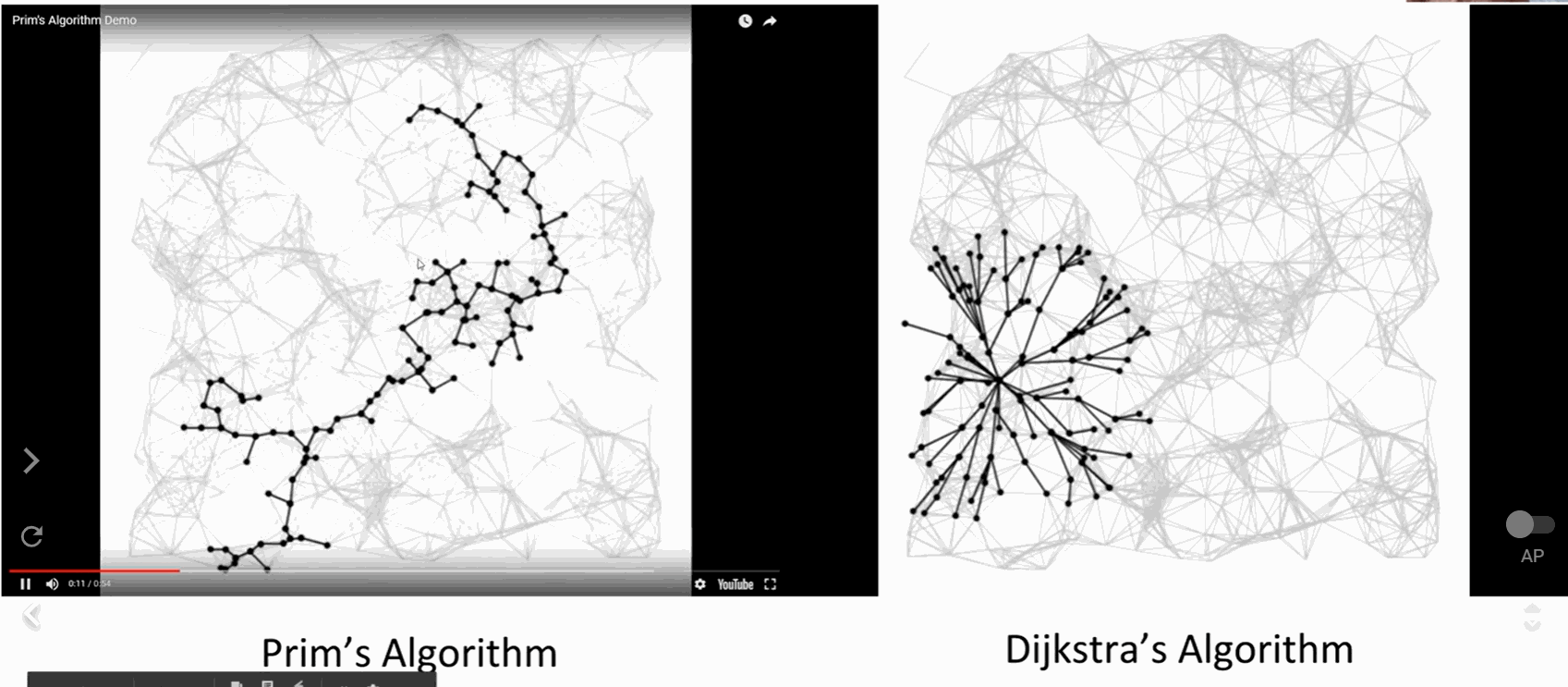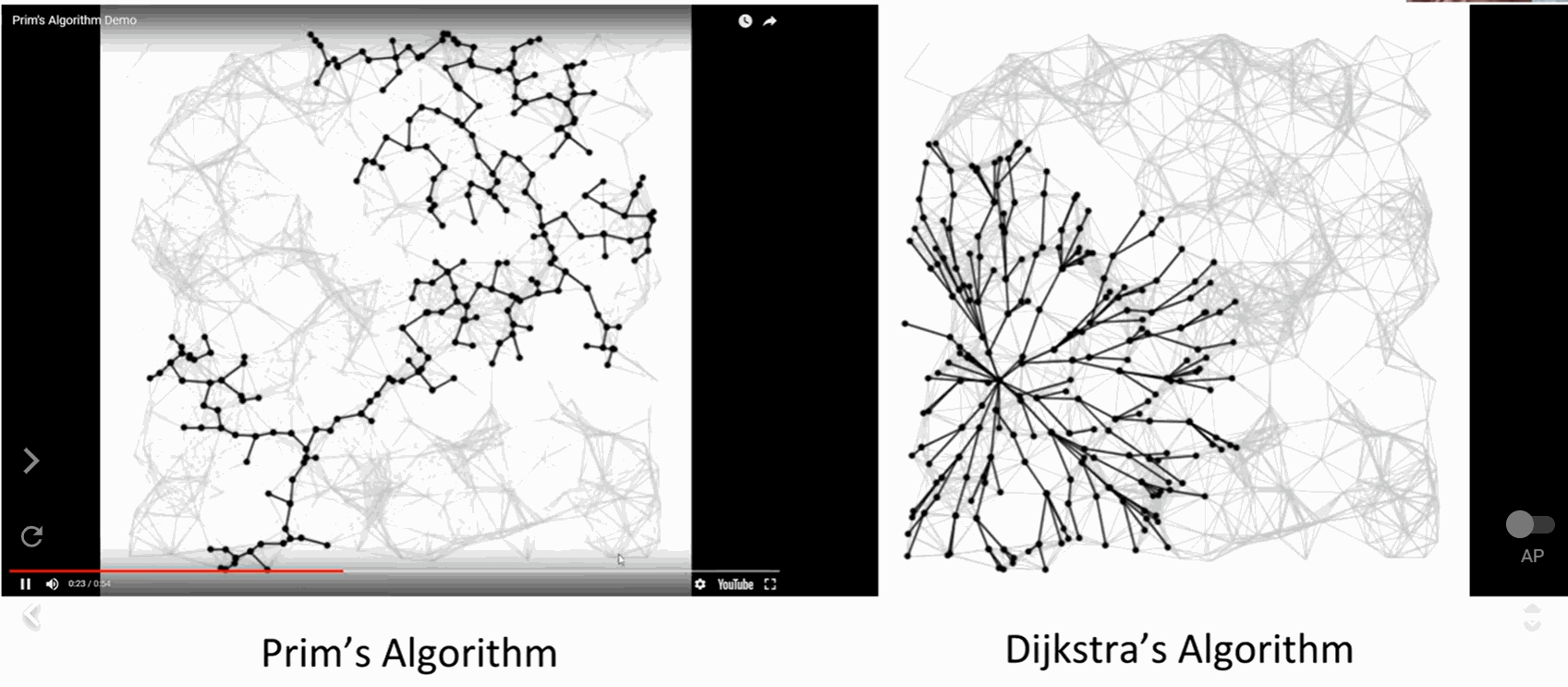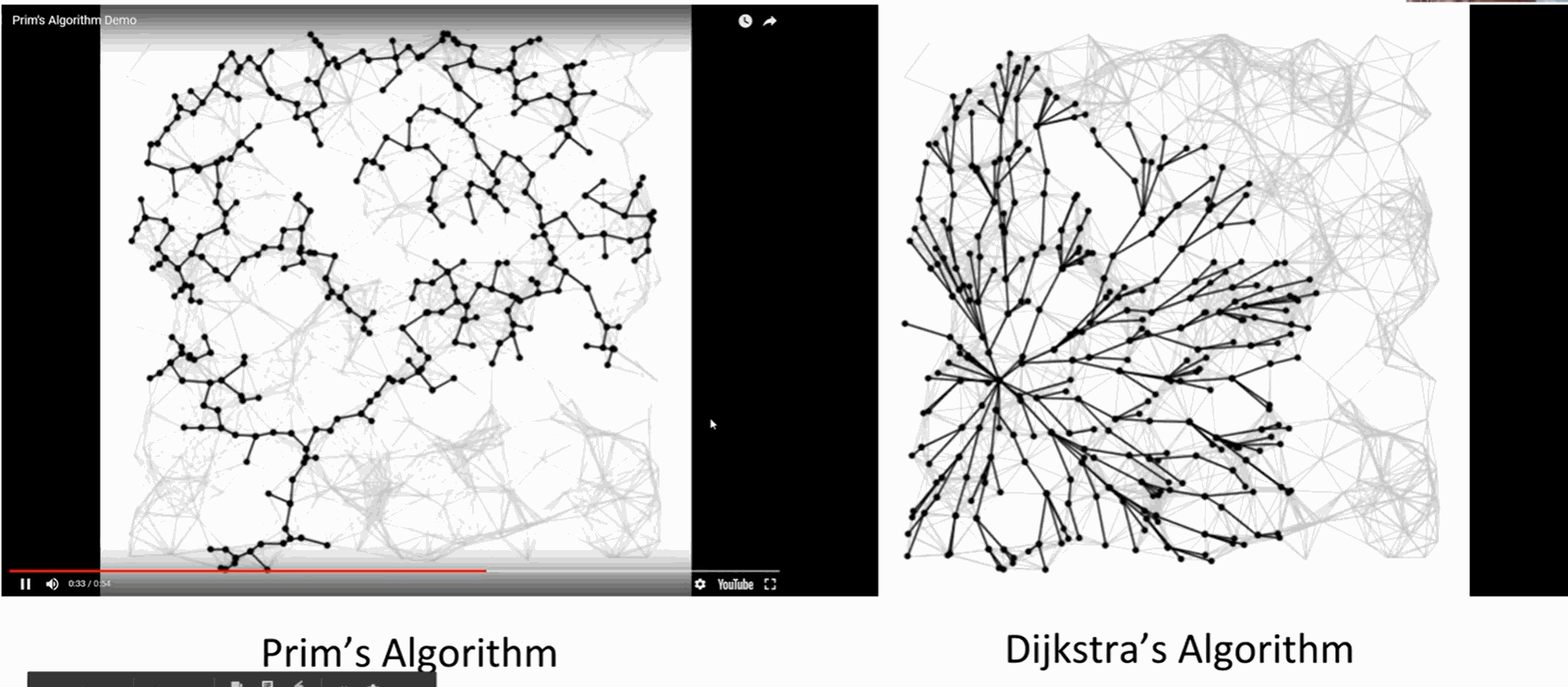
2024-03-20-17-19-38

  • 区别:

    • SPT: 从源顶点出发，所以在哪里开始很重要

    • MSP: 全局属性，与源顶点无关

代码实现

image-20240320172951394

image-20240320173004710

Kruskal算法

这是另一种从图中找到最小生成树（MST）的算法。Kruskal返回的最小生成树可能与Prim返回的不同，但是这两个算法都将始终返回一个MST；因为两者都是最小的（最优的），它们都将给出有效的最优解（它们在最小/总权重相同的情况下一样优，而且这是尽可能低的）。

该算法步骤如下：

  1. 将所有边从最轻到最重排序。
  2. 逐个考虑边（按排序顺序），如果添加该边不会形成循环，则将其添加到我们正在构建的MST中。
  3. 重复直到有 $V-1$ 条边。

Kruskal算法有效的原因是我们添加的任何边都将连接一个节点，我们可以说这个节点是一个集合的一部分，以及第二个节点，我们可以说是第二个集合的一部分。我们添加的这条边不是循环的一部分，因为我们只有在不会形成循环的情况下才会添加一条边。此外，我们按照从最轻到最重的顺序查看候选边。因此，我们要添加的这条边必须是横跨此割的最轻的边（如果存在一条更轻的边，那么它将在此之前被添加，添加这条边将导致出现循环）。因此，该算法也是通过割属性工作的。

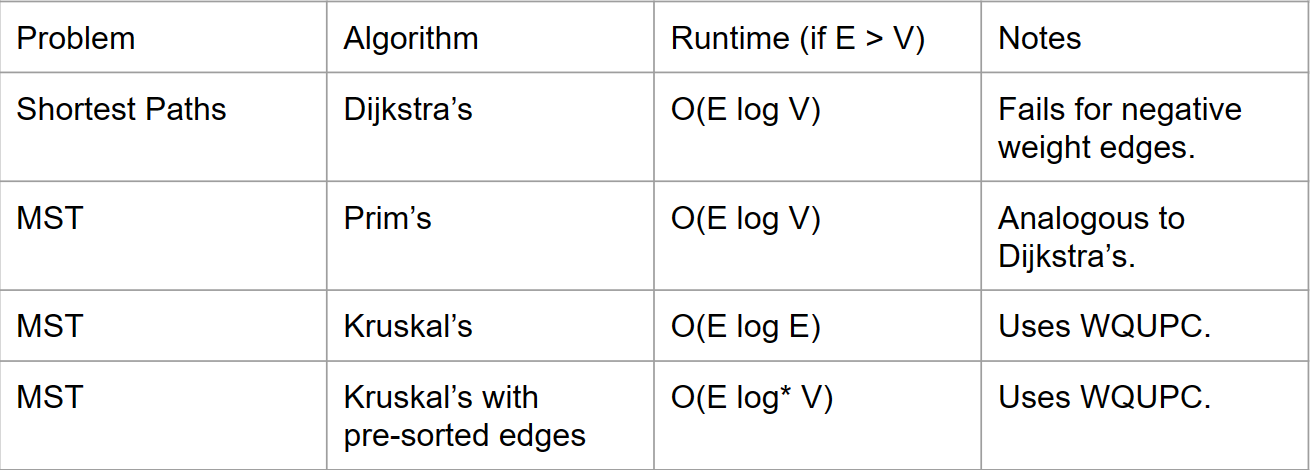
Kruskal算法运行时间为$O(|E| \log |E|)$，因为算法的瓶颈是开始时对所有边进行排序（例如，我们可以使用堆排序，其中我们将所有边插入堆中，并逐个删除最小边）。如果我们已经给出了预先排序的边并且不需要为此付出代价，那么运行时间是 $O(∣E∣log ^∗ ∣V∣)$。这是因为每当我们提出要添加的边时，我们都需要检查它是否会引入循环。我们知道如何做到这一点的一种方法是使用带路径压缩的加权快速并查集；这将有效地告诉我们两个节点是否已经连接在一起。这将花费$∣E∣$ 次调用 isConnected，每次调用的成本为$ O(log ^∗ ∣V∣)$，其中$log^*$是阿克曼函数。

2024-03-20-17-17-07

代码实现

image-20240320173029921

总结

image-20240320173106199