Uniform Partitioning 统一分区

Motivation 赋予动机

假设我们想对空间中的一组 Body 对象执行操作。例如，也许我们想问一些关于二维图像空间中的太阳体（如下图所示）的问题。

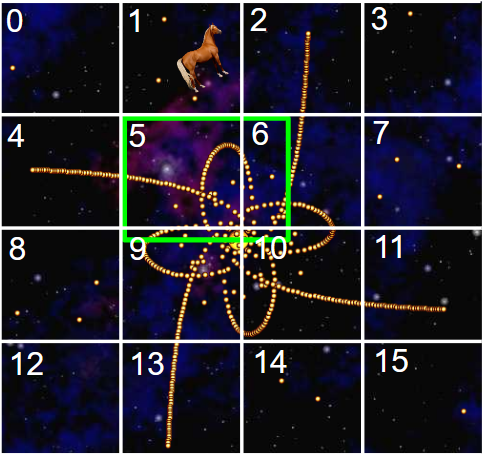
First Question: 2D Range Finding 第一个问题：2D 测距

我们可能会问的一个问题是：一个区域中有多少个对象，例如在上面突出显示的绿色矩形中？

Second Question: Nearest Neighbors 第二个问题：最近邻

我们可能会问的另一个问题是：离另一个物体最近的物体是什么，比如哪个太阳离我们的太空马最近？（通过目视检查发现的所需答案是太阳最接近其后蹄。

Initial Attempt: HashTable 初始尝试：HashTable

问题：如果我们的太阳集存储在 HashTable 中，那么找到最近邻问题的答案的运行时是什么？

解决方案：每个物体所在的桶实际上是随机的，因此我们必须遍历所有 $N$ 物品，以检查每个太阳是否可能最接近马。 Θ(N) 。

让我们试着改进，这样我们就不必看我们布景中的每一个太阳来找到我们的答案。

Second Attempt: Uniform Partitioning 第二次尝试：统一分区

哈希表的问题在于，项目的桶号实际上是随机的。哈希表绝对是无序集合。一个解决方法是确保铲斗编号仅取决于位置！

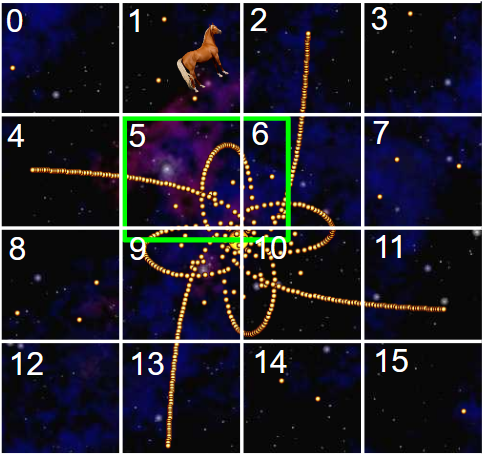
如果我们通过在图像空间上抛出一个 4x4 网格来均匀地划分图像空间，我们会得到井井有条的桶，看起来像这样（这有时也称为“空间散列”）：

这可以通过不使用对象的 hashCode() 函数来实现，而是让每个对象提供 getX() 和 getY() 函数，以便它可以计算自己的存储桶编号。

现在，我们知道我们的搜索可以限制在哪些网格单元中，我们只需要查看这些特定单元中的太阳，而不是像以前那样查看整个图像空间中的所有太阳。

一个区域中有多少个对象？：我们只需要查看存储桶 5、6、9 和 10。

哪个太阳离马最近？：首先，我们从马所在的单元格开始：1 .然后，我们可以向外移动到0、4、5、6和2。等等。

问题：使用统一分区，假设太阳均匀分布，找到最近邻问题的答案的运行时是什么？

解决方案：平均而言，运行时将比没有空间分区快 16 几倍，但不幸的是 $16/N$ 仍然 $Θ(N)$ 如此。但是，这在实践中确实效果更好。

不过，让我们看看是否有更好的方法。

QuadTrees

第三次尝试：QuadTrees

基于X或基于Y的树

搜索树相对于哈希表的一个关键优势在于树明确地跟踪项目的顺序。例如，在BST中查找最小项的时间复杂度是 Θ(logN)，但在哈希表中是 Θ(N)。让我们尝试利用这一点来为我们的目标提供更好的性能。

然而，这并不是微不足道的…为了构建一个二叉搜索树，我们需要能够比较对象。然而，在二维（或更多）空间中，一个对象在一个维度上可能是“小于”另一个对象，但在另一个维度上可能是“大于”另一个对象。那么，对于我们搜索树的目的，哪个维度应该是“较小”的和“较大”的呢？

例如，在下面的例子中，火星在x维度上“小于”地球，但在y维度上“大于”地球。

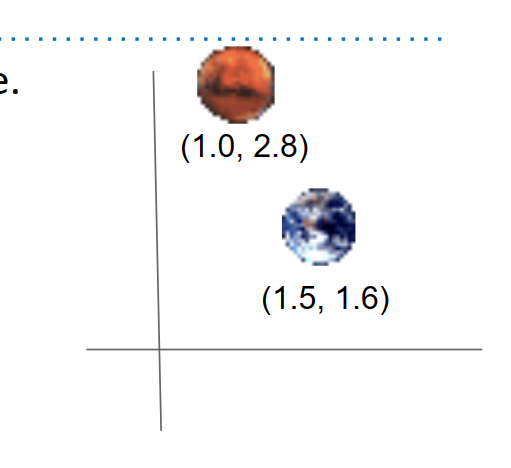
所以我们应该使用下面显示的这两种表示中的哪一种呢？请记住，我们不想任意地进行决定，因为我们需要确切地知道一个节点是否将位于树中的特定路径下，否则，我们可能会失去我们的 Θ(logN) 时间复杂度。

假设我们使用基于X的树——也就是说——我们构建一个仅查看x坐标的BST。（在组织时忽略y坐标。）对于一个更大的例子，我们可能会得到如下结果：

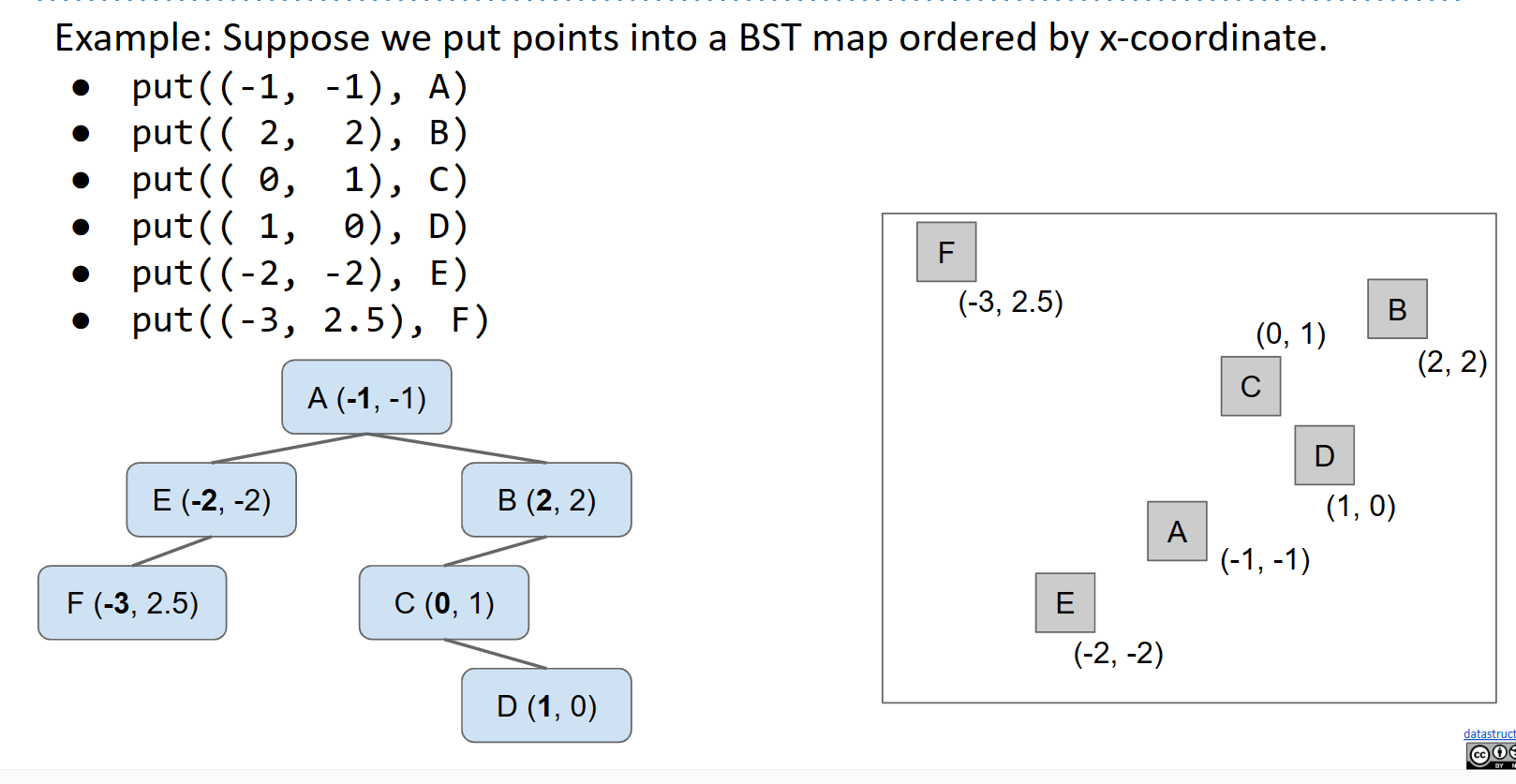
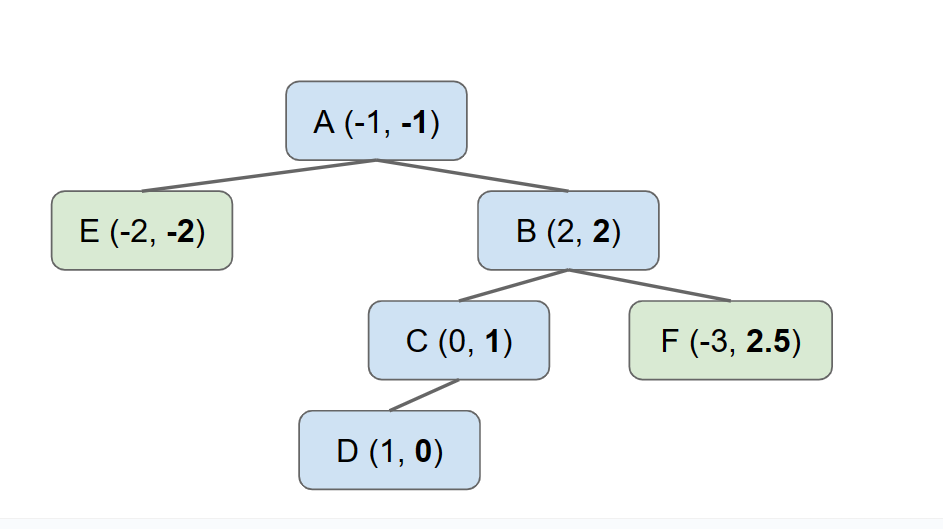
请注意，如果我们在这棵树上执行搜索，并且我们正在寻找一个x坐标小于−1的点，当我们选择左侧路径时，我们立即就能丢弃右子树中的所有内容。这相当于说，我们能够将我们的搜索空间从整个图像空间缩小到只有绿色矩形。跳过搜索树部分的能力称为“修剪”。

然而，相反地，如果我们正在寻找具有特定y坐标的点，我们的基于X的树不适用于这种类型的搜索，我们将不得不在线性搜索所有节点。

无论我们选择基于X的树表示还是基于Y的树表示，我们总是会有次优的修剪；在优化的维度中搜索将是 Θ(logN)，但在非优化的维度中搜索将是 Θ(N) 的运行时间。

QuadTree

我们可以通过同时在两个方向上进行拆分来解决这个问题。这就是QuadTree。

在这里，我们看到节点A将其周围的区域分为西北、东北、东南和西南四个区域。由于B位于A的东北象限，当我们插入B时，我们可以将其作为A的NE子节点。

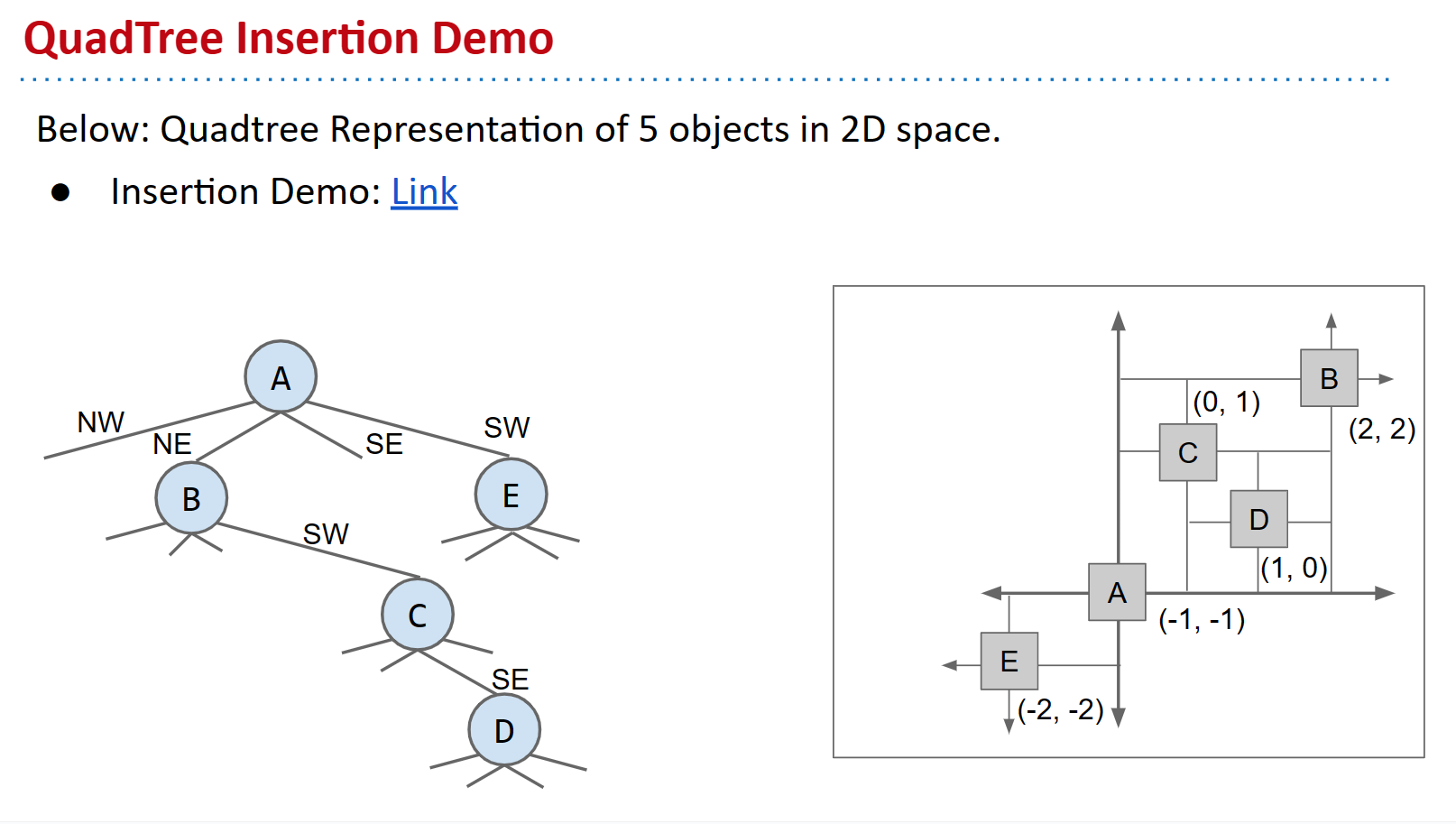
请注意，就像在BST中一样，我们插入节点的顺序决定了QuadTree的拓扑结构。

还请注意，QuadTrees是一种伪装的空间划分形式。类似于如何统一划分创建了一个完美的网格，QuadTrees通过每个节点“拥有”4个子空间来分层划分。

有效地，有许多点的空间被划分为更细分的区域，而在许多情况下，这会提供更好的性能。

使用QuadTree进行范围搜索

请注意，由QuadTree的每个节点施加的4向划分，我们仍然有之前在基于X和基于Y的树中如此有利的修剪效果！如果我们正在寻找绿色矩形内的点，从任何节点开始，我们可以决定绿色矩形是否位于一个或多个象限内，并且只探索与那些象限相对应的分支/子树。所有其他象限都可以安全地被忽略和修剪掉。下面，我们看到绿色矩形仅位于东北象限，因此西北、东南和西南象限都可以被修剪掉并留待后续探索。我们可以递归进行。

Quad-Trees非常适合于二维空间，因为只有4个象限。但是，如果我们想要进入更高维度的空间，我们将在下一章中探讨另一个能够解决这个问题的数据结构。

K-D Trees

一种将分层分区思想扩展到高于两个维度的方法是使用K-D树。它通过逐级地在所有维度之间旋转来工作。

因此，对于二维情况，它在第一级上像基于X的树一样分区，然后在下一级像基于Y的树一样，然后在第三级像基于X的树，第四级像基于Y的树，依此类推。

在第一个图中，您可以看到每个级别如何分区。在下面的图中，您可以看到树节点与二维空间中其他节点的关系。请注意当您对K-D树或四叉树运行操作时，应该考虑树结构（第一张图片）而不是二维空间（第二张图片），因为只有树包含关于级别的信息。

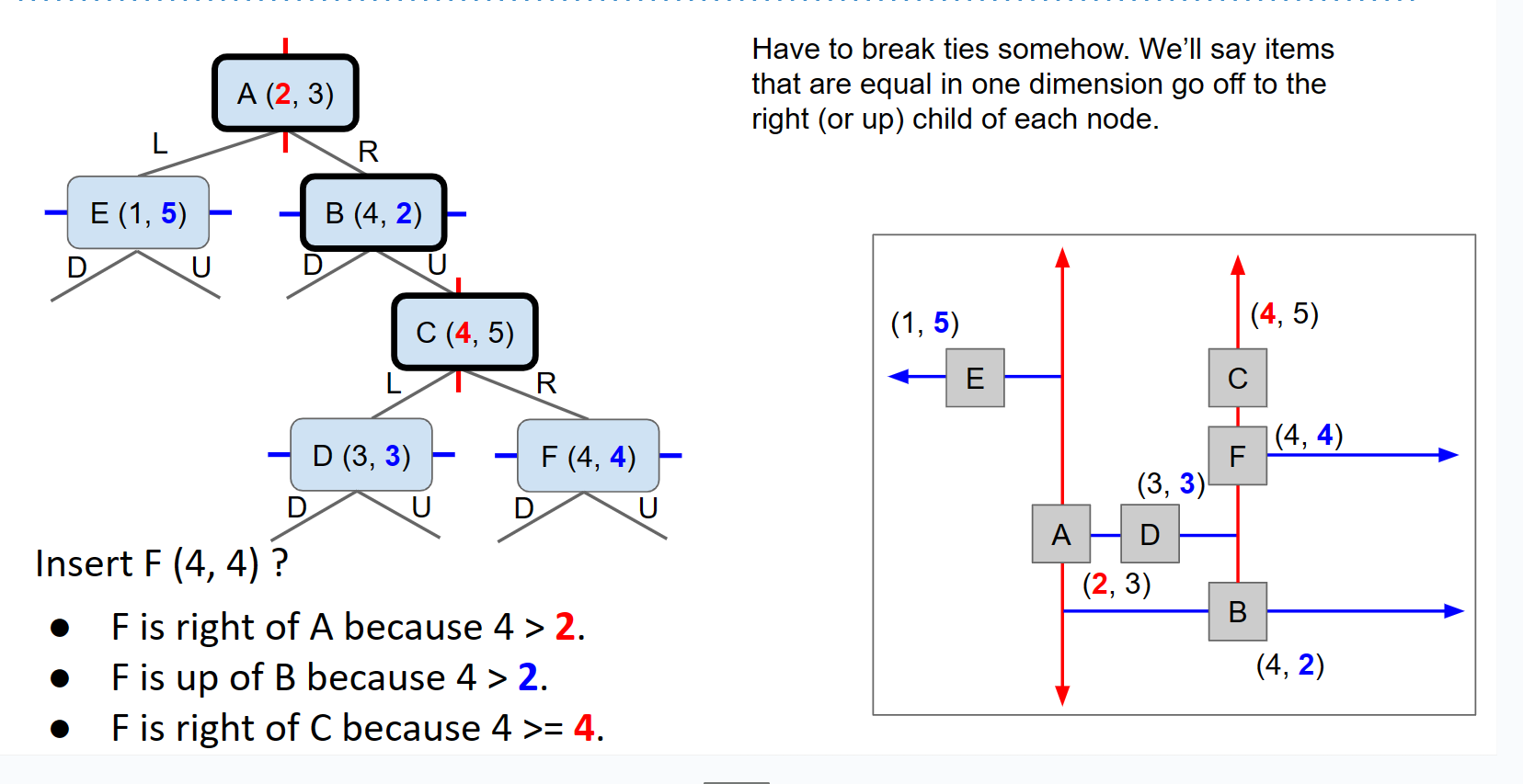
对于三维情况，它在每三个级别之间轮换三个维度，对于更高维度，依此类推。在这里，您可以看到K-D树的优点在于它更容易推广到更高维度。但是，无论维度多高，K-D树始终都将是一个二叉树，因为每个级别都被分成“大于”和“小于”。

要找到最接近查询点的点，我们在K-D树中遵循以下步骤：

从根节点开始，将该点存储为“到目前为止最佳”。计算其与查询点的距离，并将其保存为“要打败的分数”。在上图中，我们从距离标记点最近的A开始，其距离为4.5。
此节点将其周围的空间分成两个子空间。对于每个子空间，问：“在这个空间内可能找到更好的点吗？”这个问题可以通过计算查询点与我们子空间边缘之间的最短距离来回答（见下图中的虚线紫线）。
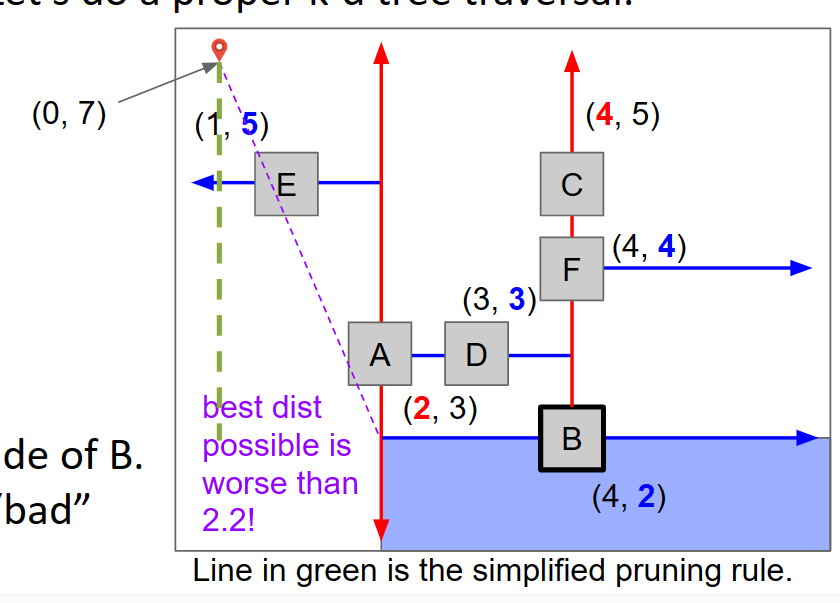
对于被确定为包含可能更好点的每个子空间，继续递归。
最后，我们的“到目前为止最佳”是最佳点；最接近查询点的点。

请参阅这些幻灯片以逐步了解。

摘要和应用

请参见上面的视频，了解本章的摘要以及所提供的数据结构的一些有趣应用。