CS61B学习笔记(二十一)-Tries

我们现在将学习一个名为 Tries 的新数据结构。这些将作为 Set 和 Map 的新实现（根据我们之前所学到的），该 Map 对某些类型的数据和信息具有一些特殊功能。

Trie的介绍

回顾

由于我们正在考虑 ADT Set和Map，让我们回顾一下到目前为止所学到的实现。过去，我们主要学习如何使用二叉搜索树或哈希表来实现这些 ADT。让我们回顾一下这两者的运行时：

• 平衡搜索树：
  • contains(x): $Θ(logN)$
  • add(x): $Θ(logN)$
• 调整单独的链接哈希表的大小：
  • contains(x) ： $Θ(1) $（假设点差均匀）
  • add(x) ： $Θ(1)$ （假设均匀点差和摊销）

我们可以看到，与 Sets 和 Maps 相关的操作的实现速度非常快。

问题：我们能做得比这更好吗？这可能取决于我们问题的性质。如果我们知道钥匙的特殊特性会怎样？

答：是的，例如，如果我们总是知道我们的键是 ASCII 字符，那么不要使用通用的 HashMap，只需使用一个数组，其中每个字符都是我们数组中的不同索引：

public class DataIndexedCharMap<V> {
    private V[] items;
    public DataIndexedCharMap(int R) {
        items = (V[]) new Object[R];
    }
    public void put(char c, V val) {
        items[c] = val;
    }
    public V get(char c) {
        return items[c];
    }
}

在这里，我们为一个采用字符键的映射创建了一个实现。值 R 表示可能的字符数（例如，ASCII 为 128）。好！通过了解Keys的范围以及它们将是什么类型的值，我们得到了一个简单而高效的数据结构。现在我们已经为字符创建了一些东西，那么字符串呢？

发明 Trie

Trie是一种非常有用的数据结构，用于可以将键分解为“字符”并与其他键（例如字符串）共享前缀的情况。

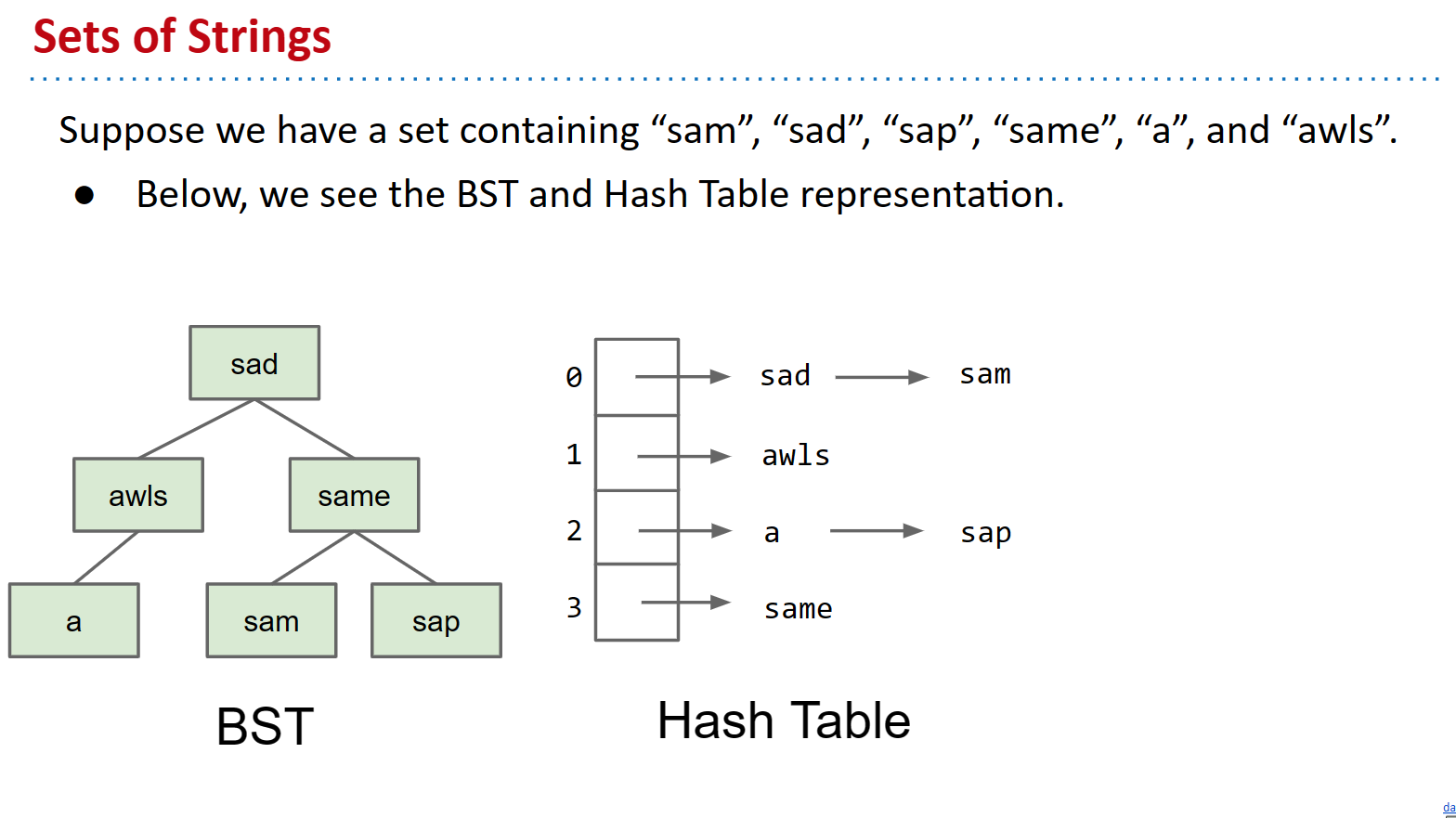
假设我们有一个包含“sam”、“sad”、“sap”、“same”、“a”和“awls”的集合。对于现有的 Set 实现，我们有以下可视化结构。我们如何使用我们已知的其他可能的数据结构来改进这一点？我们如何利用结构字符串？

以下是我们将使用的一些关键想法：

• 每个节点只存储一个字母
• 节点可以由多个Keys共享

因此，我们可以将 “sam”、“sad”、“sap”、“same”、“a” 和 “awls” 插入到包含单字符节点的树结构中。一个重要的观察结果是，这些单词中的大多数都具有相同的前缀，因此我们可以利用这些结构相似的字符串来构建我们的结构。换句话说，我们不会多次存储相同的前缀（例如“sa-”）。

看看下面的图表，看看 trie 会是什么样子：

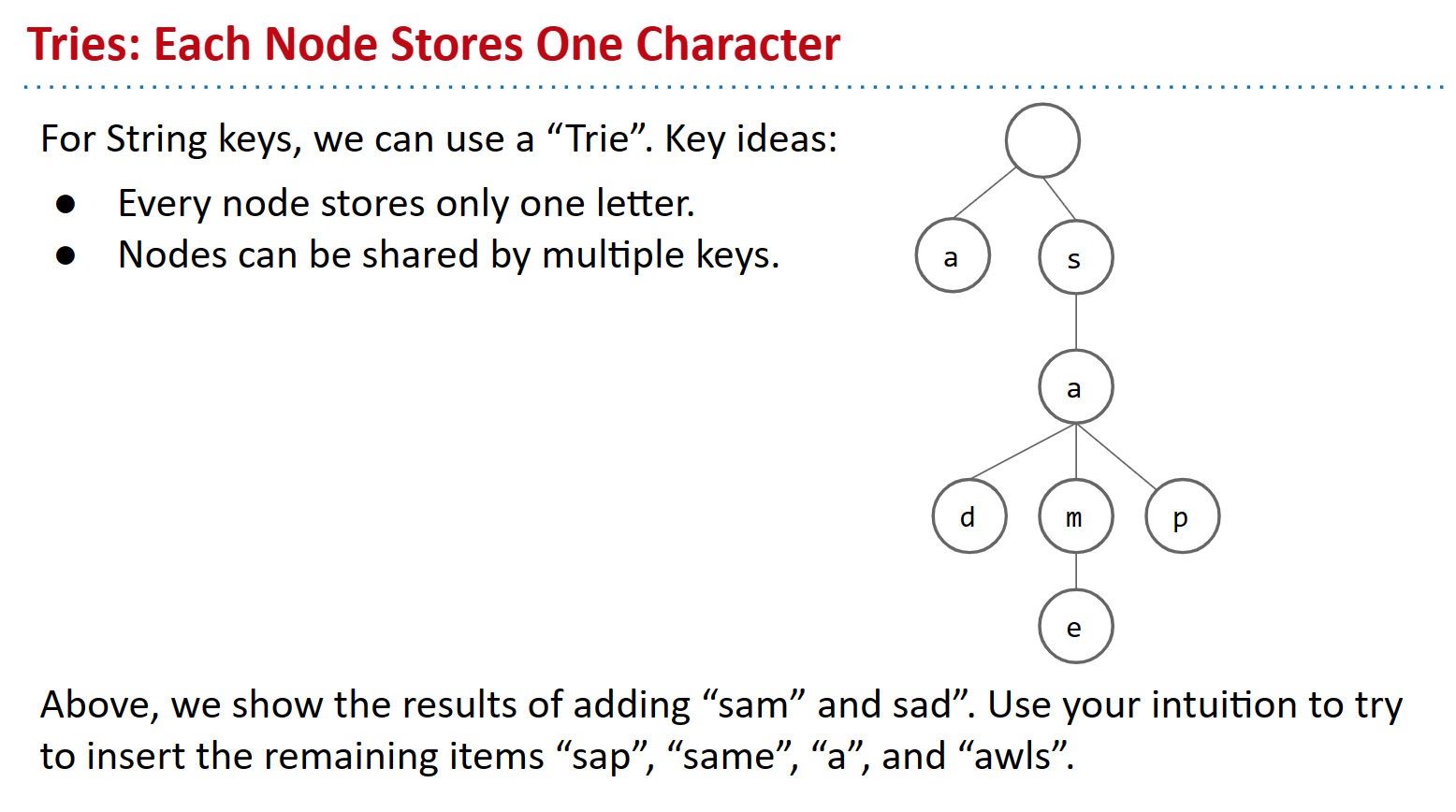
尝试通过将Keys的每个“字符”存储为节点来工作。共享公共前缀的Keys共享相同的节点。要检查 trie 是否包含键，请沿着正确的节点从根部向下走。

由于我们要共享节点，我们必须想出某种方法来表示哪些字符串属于我们的集合，哪些不属于我们的集合。我们将通过将每个字符串的最后一个字符的颜色标记为蓝色来解决这个问题。请在下面观察我们的最终策略。

假设我们已经将字符串插入到我们的集合中，并且我们最终得到了上面的 trie，我们必须弄清楚搜索在我们当前的方案中将如何工作。为了搜索，我们将遍历我们的尝试，并在向下时与字符串的每个字符进行比较。因此，只有两种情况我们无法找到字符串;要么最后一个节点是白色的，要么我们从树上掉下来。

• contains("sam") ：true，蓝色节点
• contains("sa") ：false，白色节点
• contains("a") ：true，蓝色节点
• contains("saq") ： 假的，从树上掉下来的

练习 15.1.2.将字符串“ants”、“zebra”、“potato”和“sadness”添加到上面的 trie 中。绘制出生成的 trie 结构。

练习 15.1.3.想一想将 trie 用作地图与将 trie 用作集合之间的区别。（如果有的话）实现会有所不同吗？

在这里查看创建 trie 地图的动画演示。

总结

一个关键的要点是，当我们为问题添加特异性时，我们通常可以通过添加额外的约束来改进通用数据结构。例如，我们改进了 HashMap 的实现，将键限制为只能是 ASCII 字符，从而创建了非常高效的数据结构。

• ADT 和特定实现之间是有区别的。例如，Disjoint Sets 是一个 ADT：任何 Disjoint Sets 都具有 和 connect(x, y) isConnected(x, y) 的方法。有四种不同的方法可以实现这些方法：快速查找、快速并集、加权 QU 和 WQUPC。
• Trie 是专门用于字符串的 Sets 和 Maps 的特定实现。
  • 我们给每个节点一个字符，每个节点可以是 trie 中多个键的一部分。
  • 只有当我们碰到一个未标记的节点或者从树上掉下来时，搜索才会失败
  • Retrieval tree的缩写，几乎每个人都将其发音为“try”，但爱德华·弗雷德金建议将其发音为“树”

Trie的实现

实现

让我们实际尝试构建一个Trie。我们将采用第一种方法，即每个节点存储一个字母、其子节点和一个颜色的想法。由于我们知道每个节点键是一个字符，我们可以使用之前定义的DataIndexedCharMap类来映射所有节点的子节点。请记住，每个节点最多可以有可能字符数等于其子节点数。

public class TrieSet {
   private static final int R = 128; // ASCII
   private Node root;    // trie的根节点

   private static class Node {
      private char ch;  
      private boolean isKey;   
      private DataIndexedCharMap next;

      private Node(char c, boolean blue, int R) {
         ch = c; 
         isKey = blue;
         next = new DataIndexedCharMap<Node>(R);
      }
   }
}

聚焦于具有一个子节点的单个节点，我们可以观察到它的next变量，即DataIndexedCharMap对象，如果我们树中的节点具有相对较少的子节点，则将具有大多数空链接。我们将有128个链接，其中127个等于null，1个被使用。这意味着我们浪费了大量的多余空间！我们将进一步探讨替代表示方法。

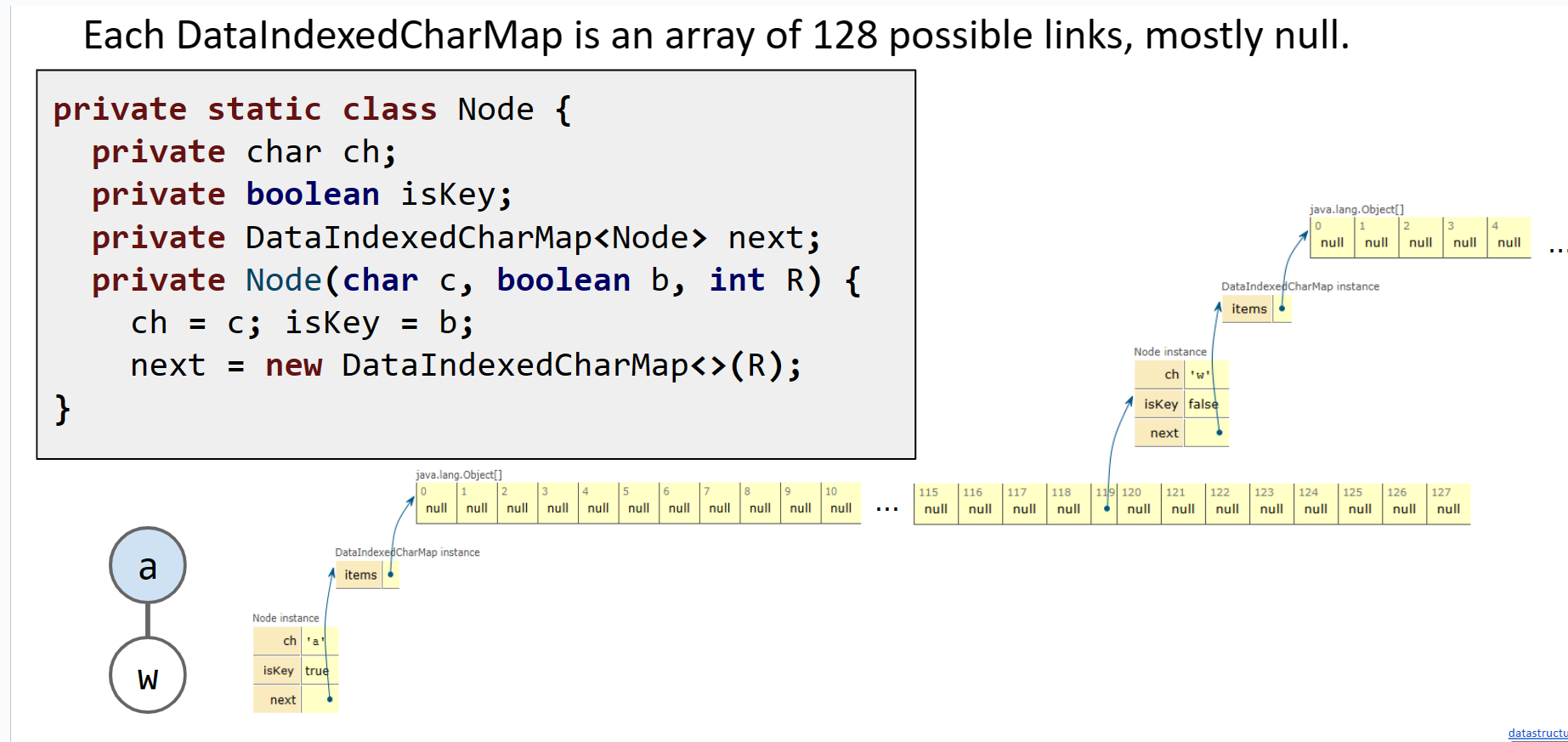
但我们可以做出重要观察：只有当该字符存在时，每个链接才对应一个字符。因此，我们可以删除节点的字符变量，而是根据其在父DataIndexedCharMap中的位置确定字符的值。

public class TrieSet {
   private static final int R = 128; // ASCII
   private Node root;    // trie的根节点

   private static class Node {
      private boolean isKey;   
      private DataIndexedCharMap next;

      private Node(boolean blue, int R) {
         isKey = blue;
         next = new DataIndexedCharMap<Node>(R);
      }
   }
}

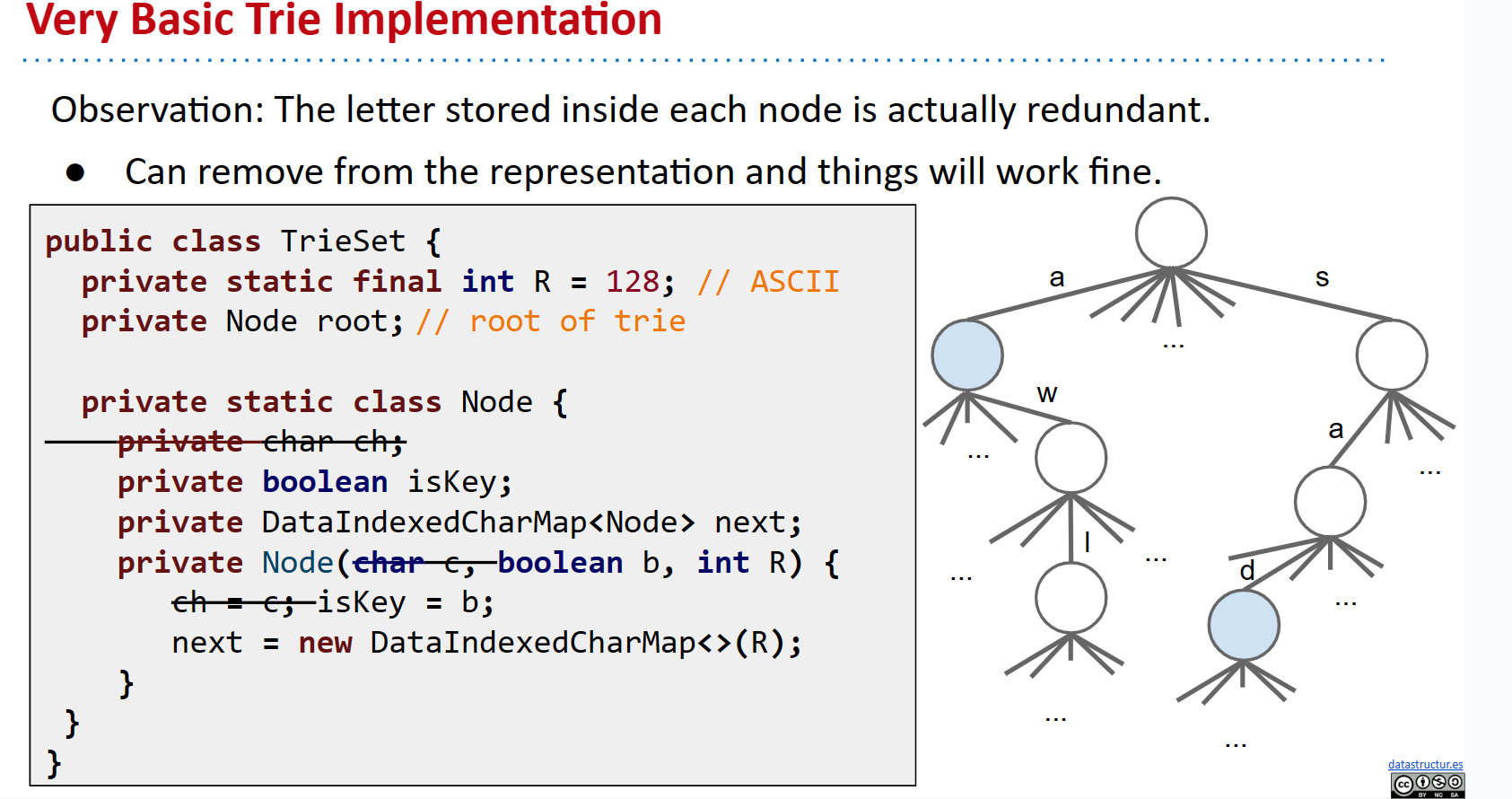
Exercise 15.2.1. 提出一种解决空间过度使用的解决方案。提示：尝试使用我们之前讨论过的一些实现。

性能

对于具有N个键的Trie，我们的Map/Set操作的运行时如下：

• 添加：
  • $Θ(1)$
• 包含：
  • $Θ(1)$

为什么会这样？我们的trie中有多少项并不重要，运行时始终与键的数量无关。这是因为在最坏的情况下，我们只遍历一个键的长度，这与trie中的键的数量无关。因此，让我们通过可以测量的测量来查看运行时；用键的长度L表示：

• 添加：
  • $ Θ(L) $
• 包含：
  • $O(L)$

我们实现了恒定的运行时，而无需担心摊销调整时间或键的均匀分布，但正如我们上面提到的那样，我们当前的设计非常浪费，因为即使该字符不存在，每个节点都包含一个数组。

子节点跟踪

我们遇到的问题是来自我们实现的DataIndexedCharMap对象的空间浪费，用于跟踪每个节点的子节点。这种方法的问题在于我们将初始化许多不包含任何子节点的空位。

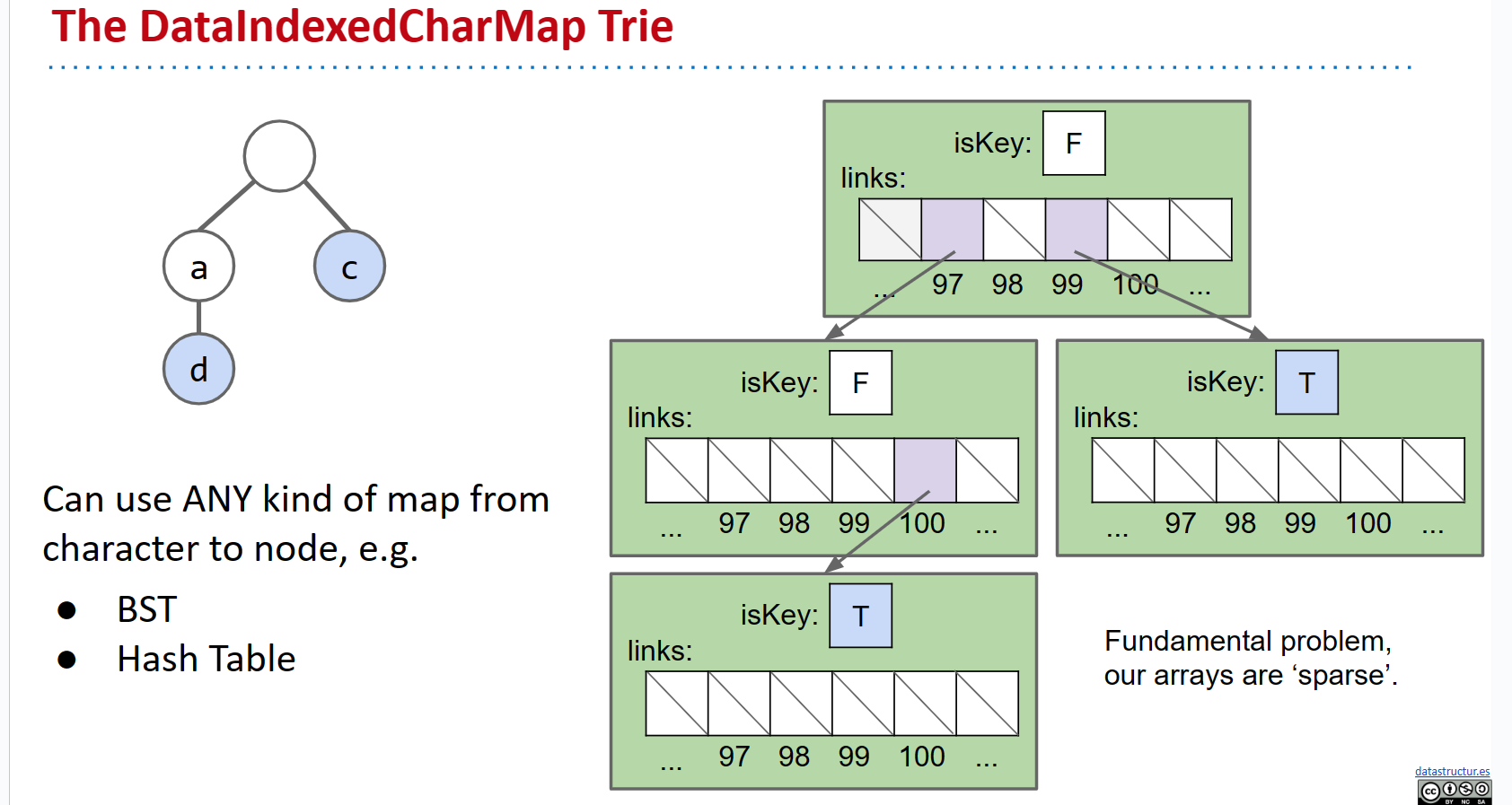
备选方案1： 基于哈希表的Trie。这不会创建128个位置的数组，而是仅在必要时初始化默认值，并根据负载因子调整数组的大小。

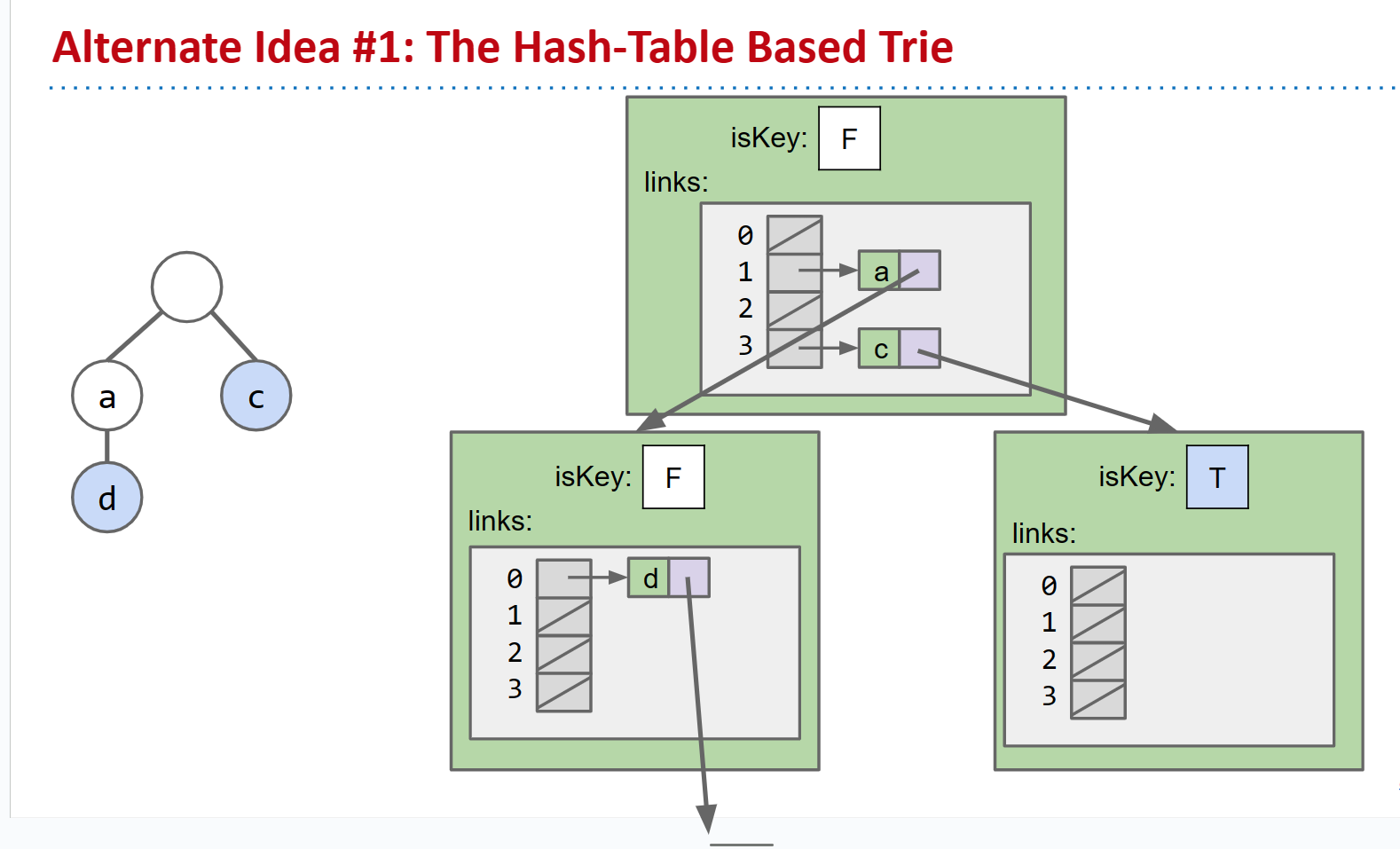
备选方案2： 基于BST的Trie。同样，仅在必要时才会创建子节点指针，并且我们将在BST中存储子节点。显然，我们仍然需要担心在这个BST中搜索的运行时，但这不是一个坏的方法。

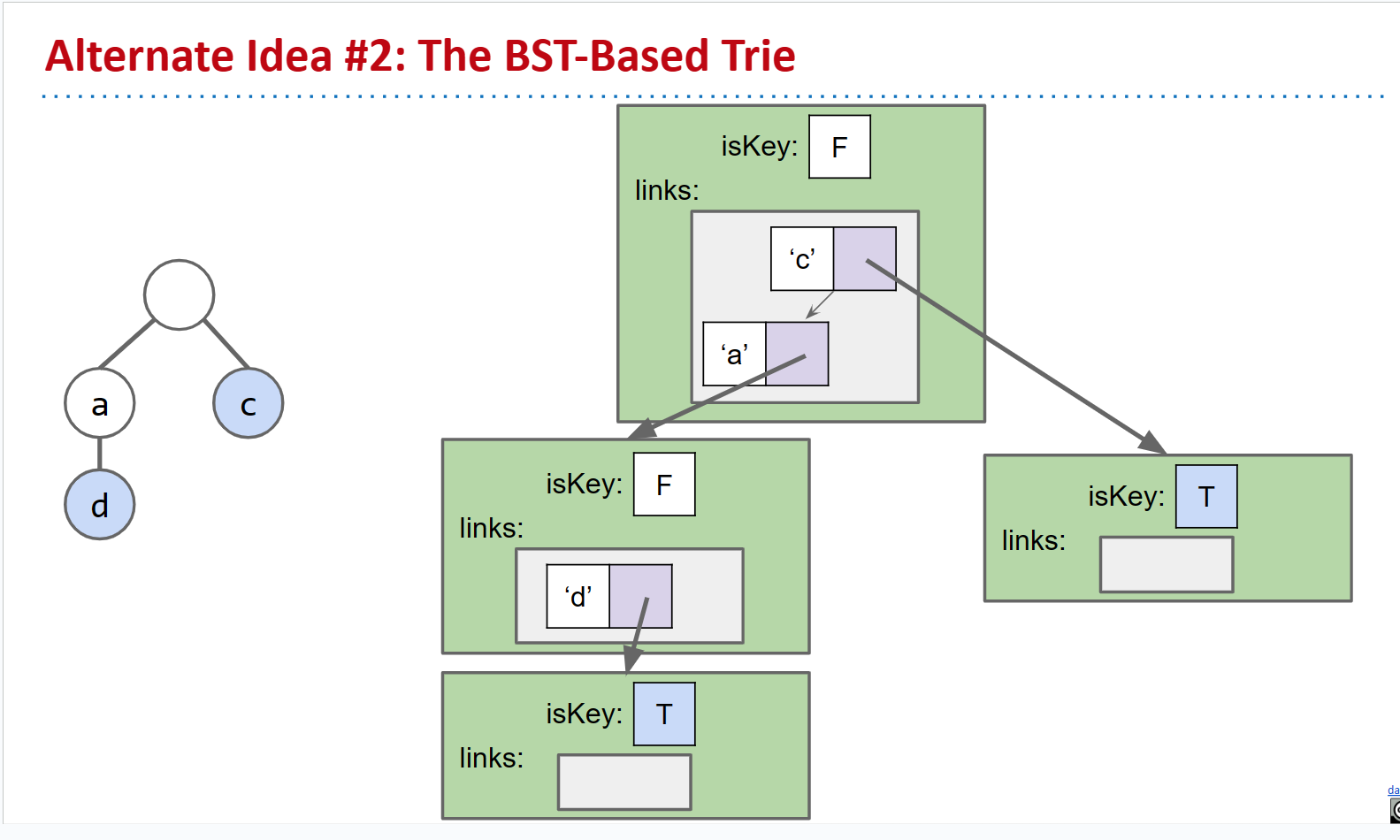
当我们实现Trie时，我们必须选择一个映射到我们的子节点的映射。Map是一个ADT，因此我们还必须选择映射的底层实现。这给我们重申了什么？在我们尝试创建ADT时，实现和ADT之间存在一个抽象屏障。这种抽象屏障使我们能够利用每种实现在尝试满足ADT行为时所提供的优势。让我们考虑每种优势：

DataIndexedCharMap

• 空间：每个节点128个链接
• 运行时：$ \Theta(1) $

BST

• 空间：每个节点C个链接，其中C是子节点的数量
• 运行时：$ O(\log R) $，其中R是字母表的大小

哈希表

• 空间：每个节点C个链接，其中C是子节点的数量
• 运行时：$ O(R) $，其中R是字母表的大小

注：BST和哈希表中每个链接的成本较高；R是一个固定数（这意味着我们可以将运行时视为常量）。

我们可以得出一些结论。存在轻微的内存和效率折衷（与BST/哈希表相比DataIndexedCharMap）。Trie操作的运行时仍然是常数，没有任何注意事项。Trie将特别适用于一些特殊操作。

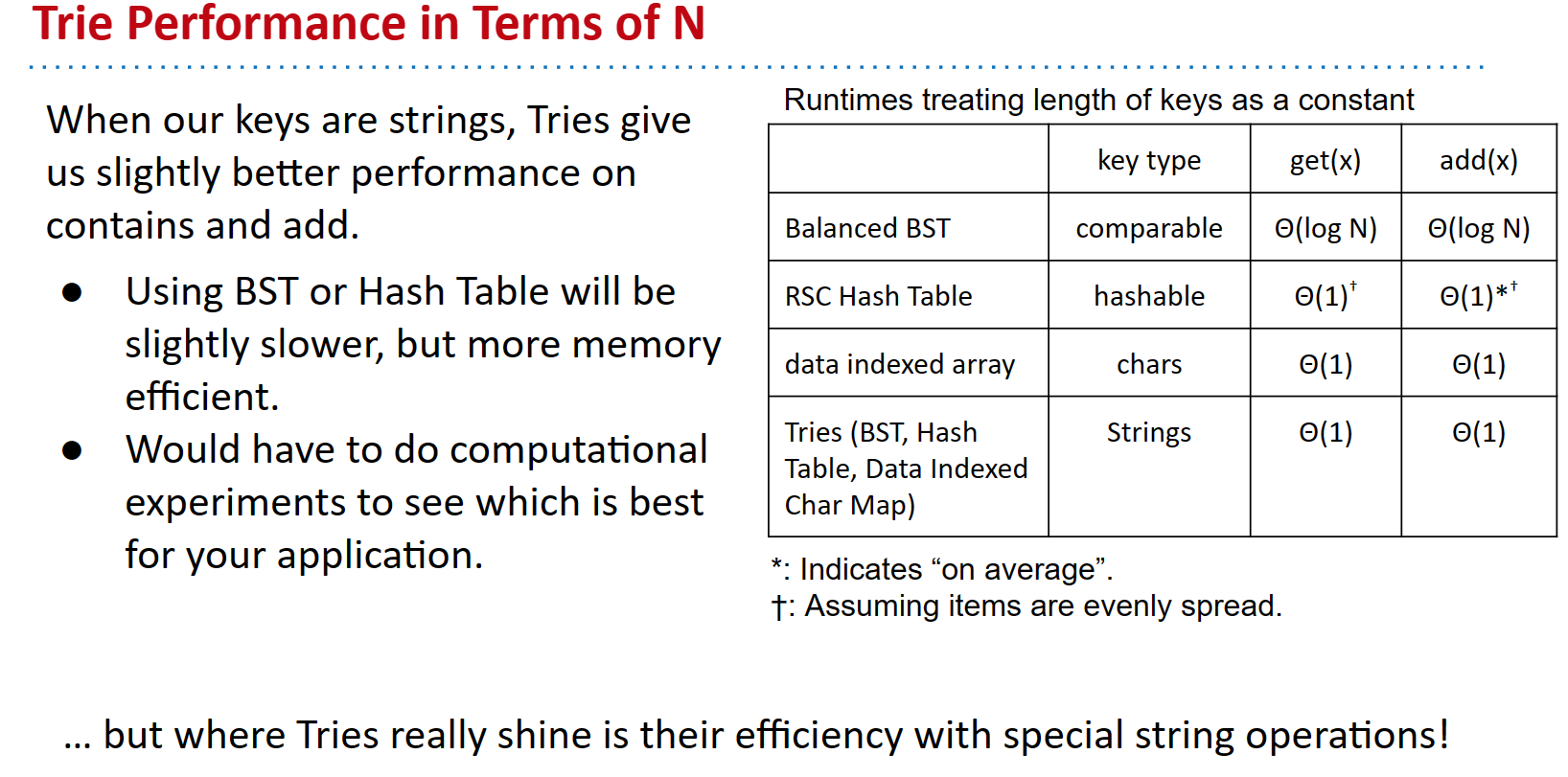
字符串操作

回顾我们对Trie和其他数据结构之间的比较。我们可以看到，Trie提供了常数时间的查找和插入，但它们实际上是否比BST或哈希表表现得更好呢？可能不是。对于每个字符串，我们必须遍历每个字符，而在BST中，我们可以立即访问整个字符串。那么，Trie有什么好处呢？

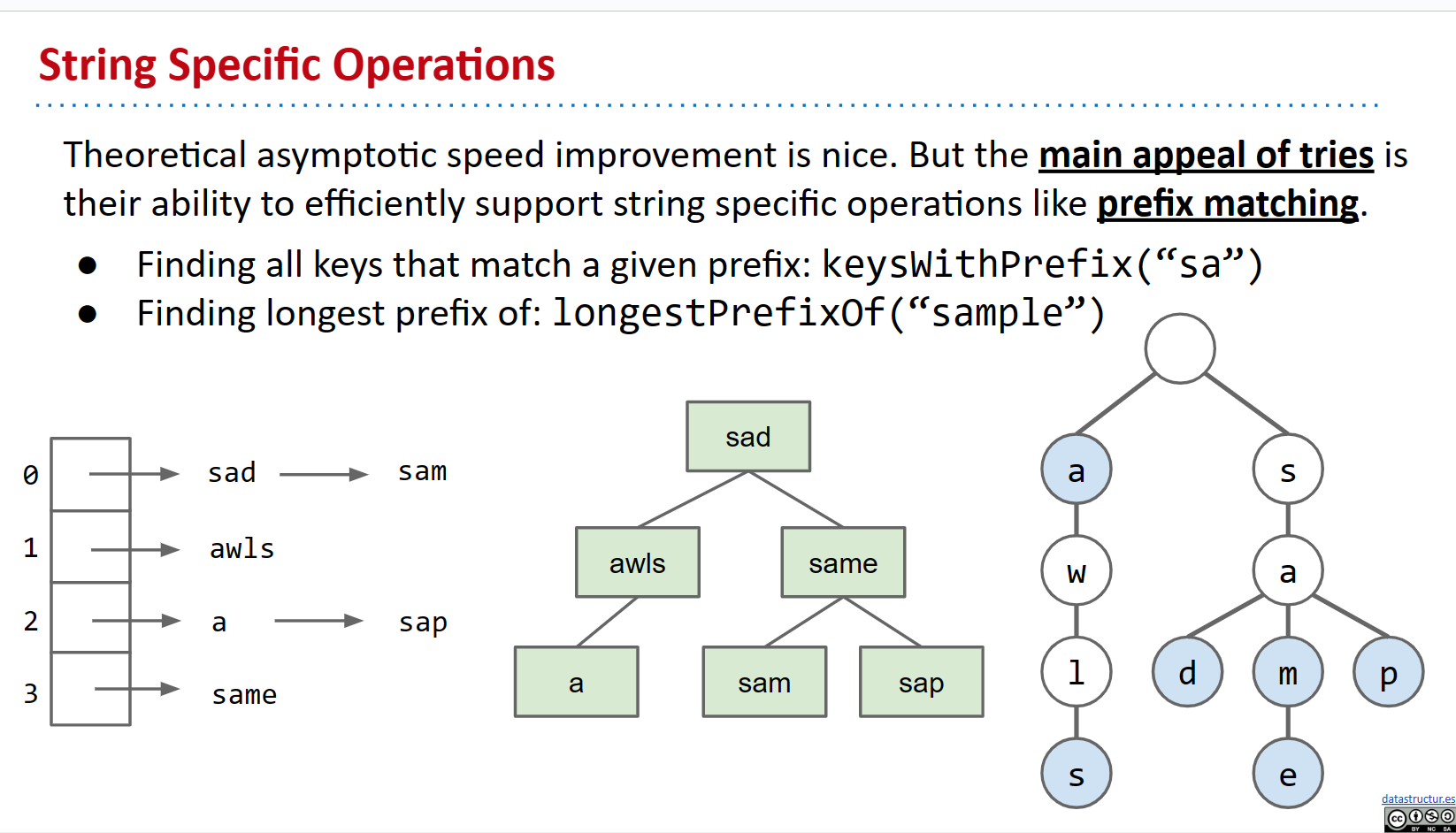
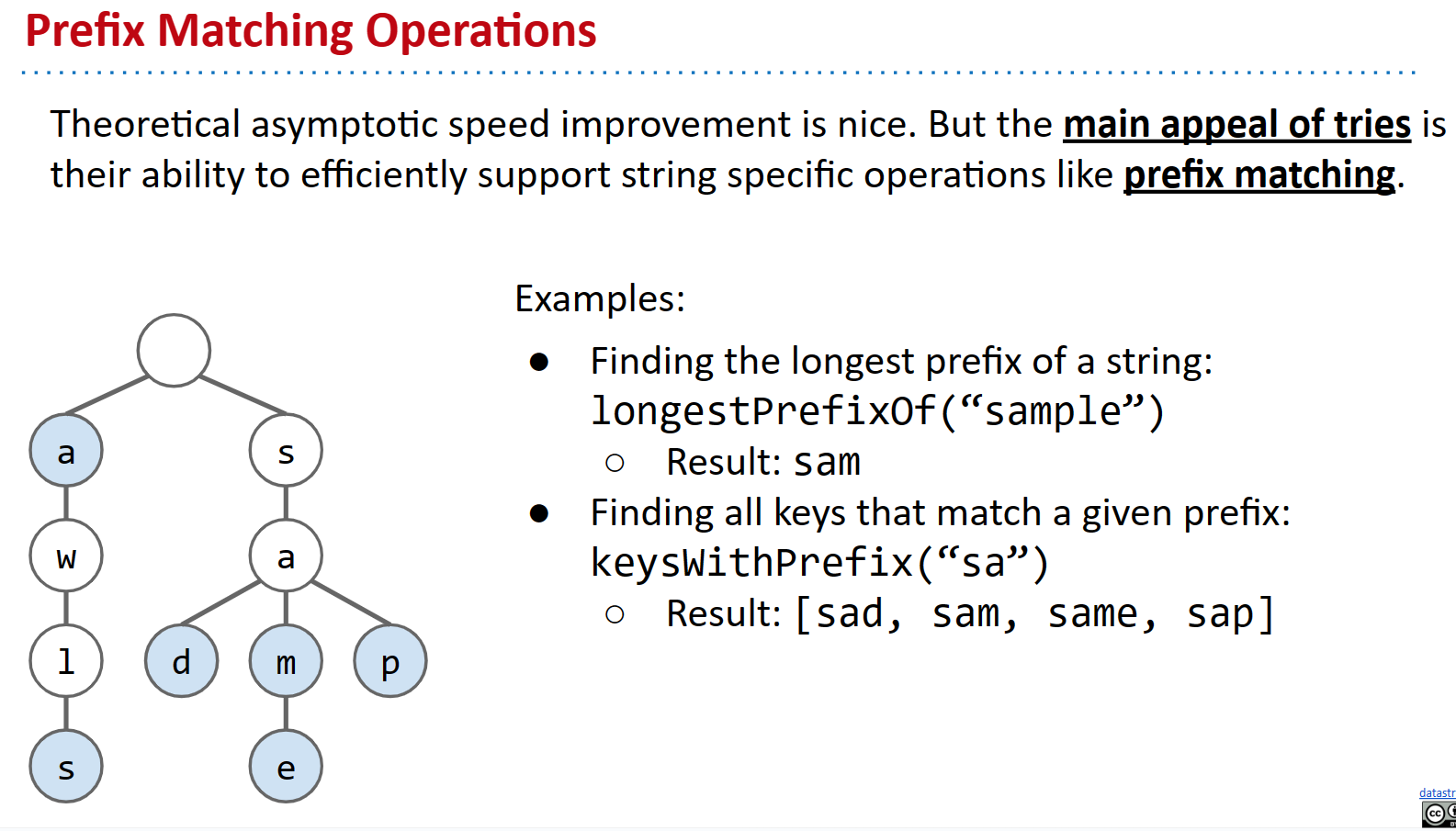
前缀匹配

Trie的主要吸引力在于能够高效支持特定的字符串操作，比如前缀匹配。你可以想象为什么Trie使这个操作变得非常高效！假设我们要找到最长的前缀。只需取出你要查找的单词，将每个字符与trie中的字符进行比较，直到无法再继续。同样地，如果我们想要keyWithPrefix，我们可以遍历到前缀的末尾，并返回trie中所有剩余的键。

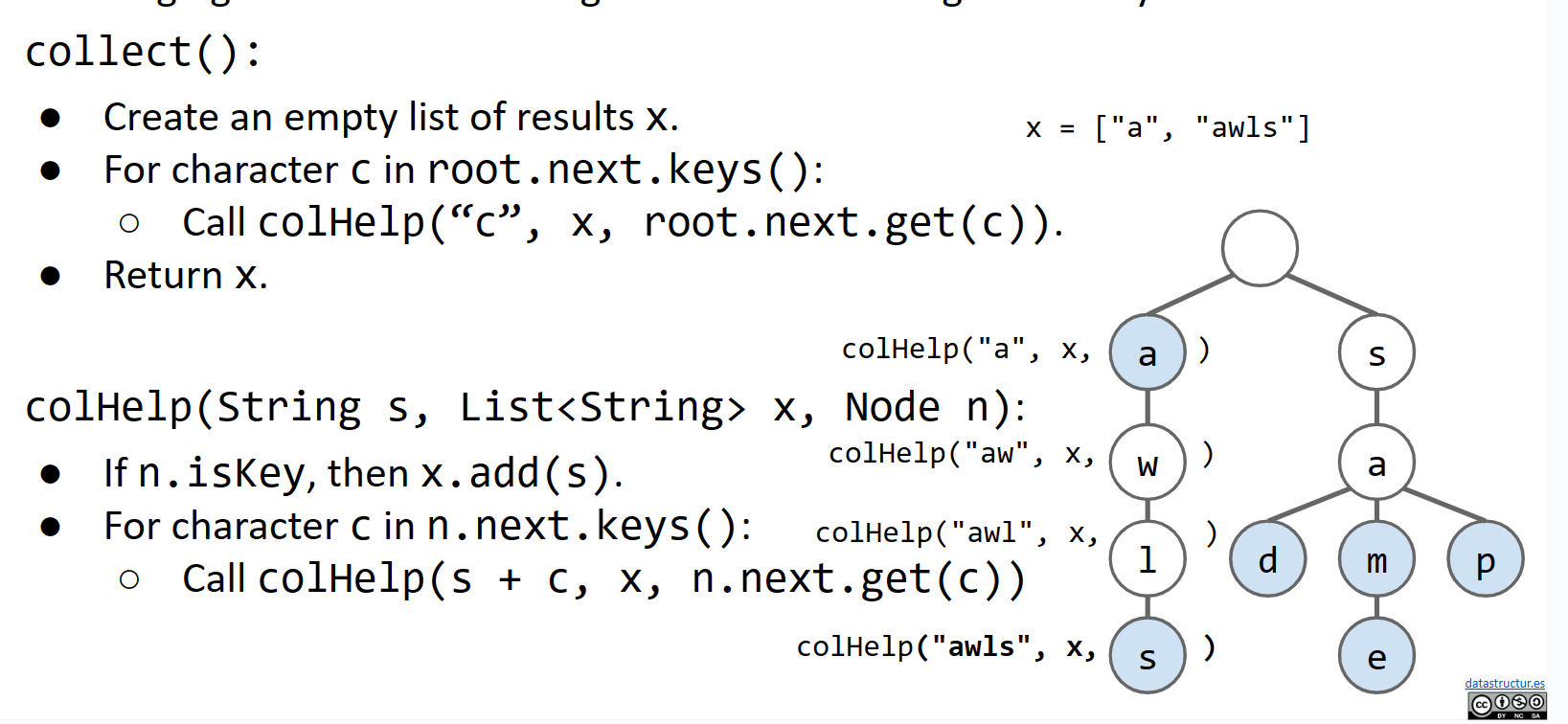
让我们尝试定义一个方法collect，它返回Trie中的所有键。伪代码如下：

collect():
    创建一个空结果列表x
    对于根节点下的每个字符c：
        调用colHelp(c, x, root.next.get(c))
    返回x

colHelp(String s, List<String> x, Node n):
    如果n是键：
        x.add(s)
    对于n下的每个字符c：
        调用colHelp(s + c, x, n.next.get(c))

我们首先在父函数内初始化我们的值，然后创建一个递归辅助函数，以便在递归调用过程中传递更多的参数。如果当前字符串是一个键，我们只添加当前字符串，否则我们将字符连接到当前遍历的字符串/路径，并调用下一个子节点的辅助函数。

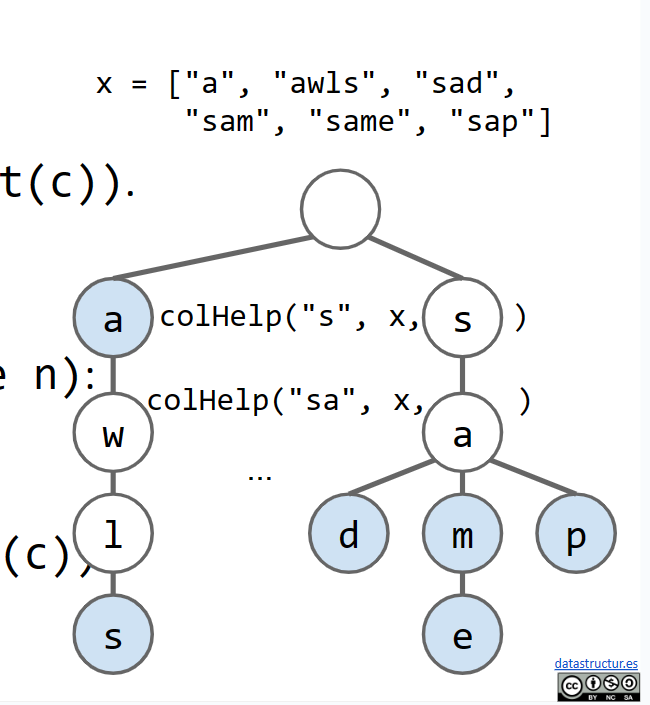
现在，我们可以尝试编写keysWithPrefix方法，它返回包含作为参数传入的前缀的所有键。我们将大量借鉴上面的collect方法。

keysWithPrefix(String s):
    找到前缀的末尾，命名为alpha
    创建一个空列表x
    对于alpha.next中的每个字符：
        调用colHelp("sa" + c, x, alpha.next.get(c))
    返回x

Exercise 15.3.1. 编写longestPrefixOf的伪代码。这将是一个你可以在实验室中完成的练习。确保观看关于如何实现其他方法的视频。

自动补全

当你在任何搜索浏览器中输入文本时，例如Google，总会有关于你即将输入内容的建议。这非常有帮助和方便。比如，当我们搜索”How are you doing”时，如果我们只输入”how are”到google，我们会看到它建议这个确切的查询。

实现这一功能的一种方法是使用Trie！我们将建立一个从字符串到值的映射。

• 值将表示Google认为该字符串有多重要（可能是频率）
• 有效地存储数十亿个字符串，因为它们共享节点，减少了冗余
• 当用户输入查询时，我们可以调用keysWithPrefix(x)方法，并返回具有最高值的10个字符串

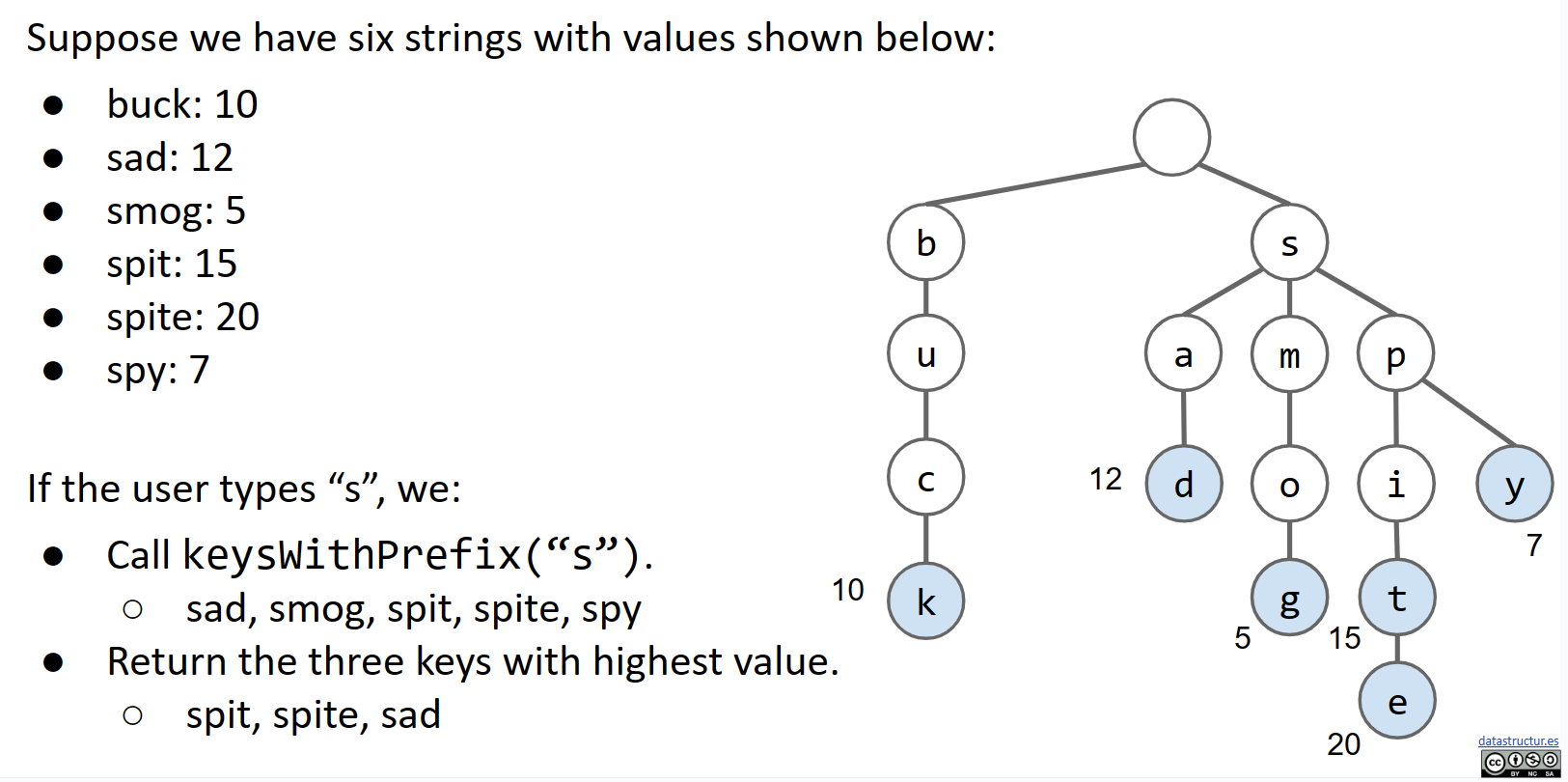
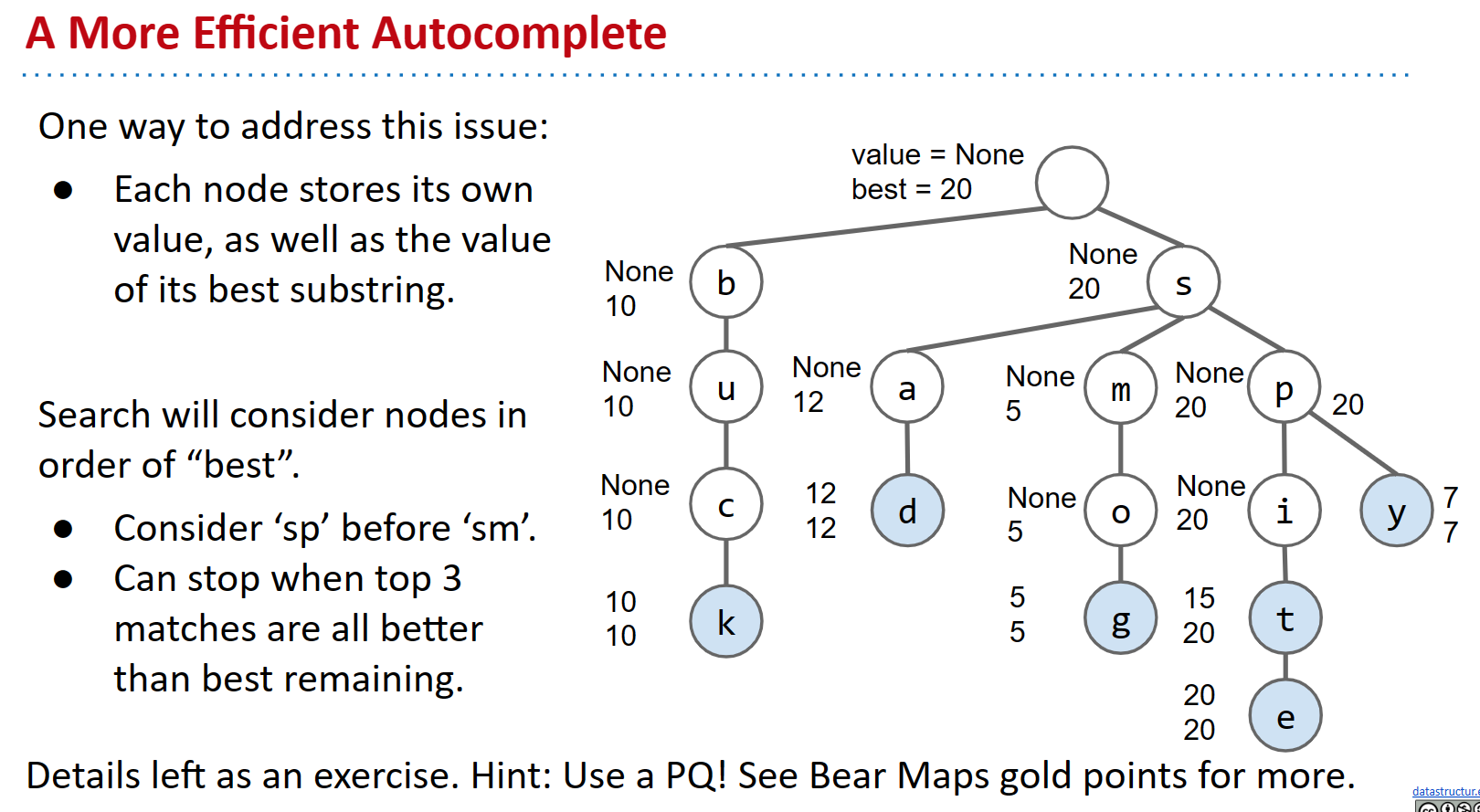
这个系统的一个主要缺陷是如果用户输入的是长度较短的字符串。你可以想象当实际上我们只想要10个键时，以输入作为前缀的键的数量可能达到了百万级别。解决这个问题的一个可能的方法是在每个节点中存储子字符串的最佳值。然后，我们可以按照最佳值的顺序考虑子节点。

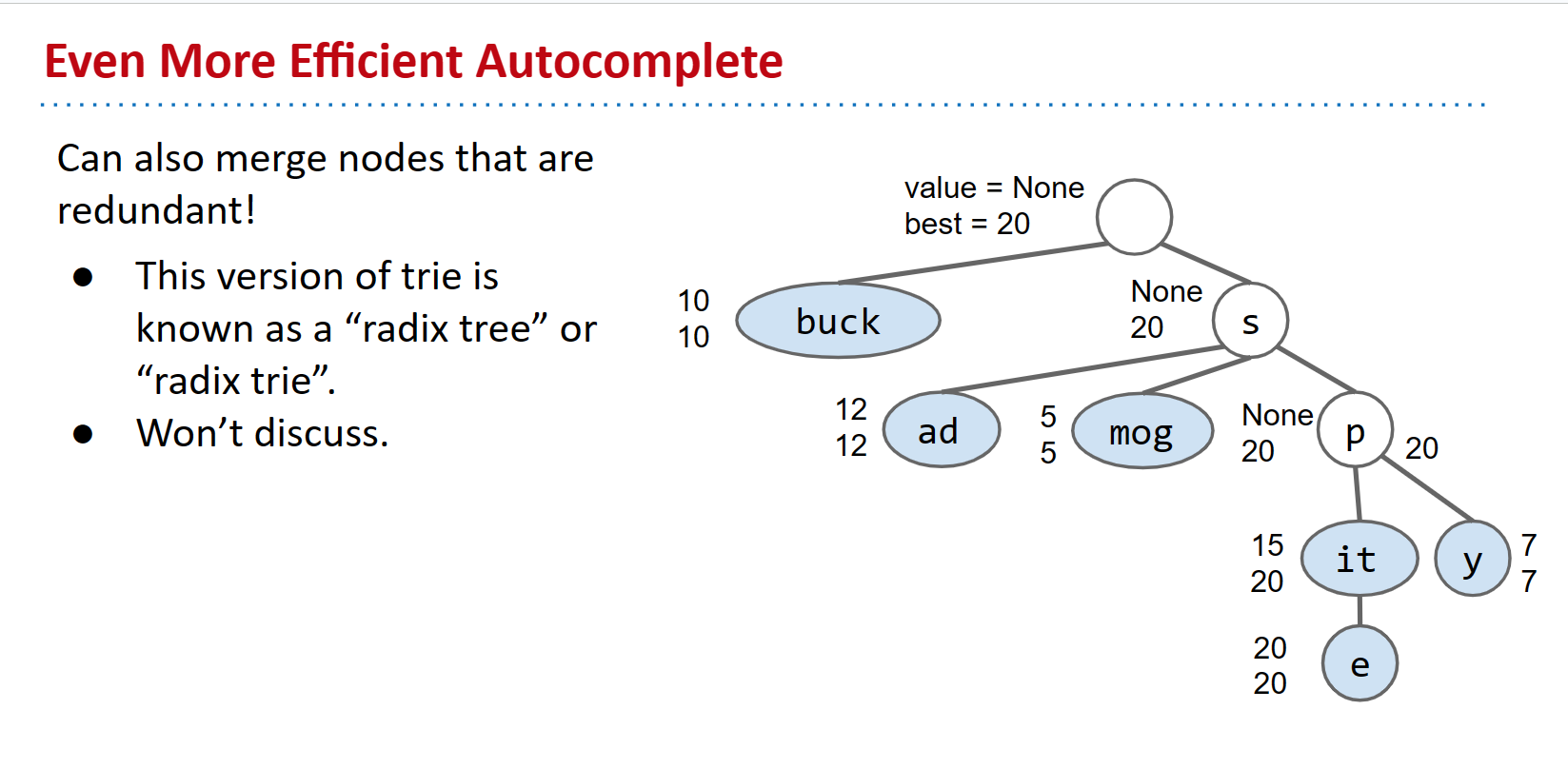
另一个优化是合并多余的节点。这将给我们一个”基数Trie”，它在每个节点中保存字符以及字符串。我们不会深入讨论这个问题。

Exercise 15.3.2. 考虑将子字符串的最佳值添加到节点中将添加什么。你如何使用优先队列创建算法？

总结

了解存储的数据类型可以让你在创建高效的数据结构时拥有巨大的优势。特别是对于实现Map和Set，如果我们知道所有键都是字符串，我们可以使用Trie：

• 从理论上讲，Trie在搜索和插入方面的性能优于哈希表或平衡搜索树
• 有关如何存储trie的每个节点的子节点的更多实现，特别是三种。这三种方法都不错，但哈希表是最自然的方法
  • DataIndexedCharMap（缺点：空间过度使用，优点：速度高效）
  • Bushy BST（缺点：子节点搜索较慢，优点：空间高效）
  • 哈希表（缺点：每个链接的成本更高，优点：空间高效）
• 在实践中，Trie实际上可能不会更快，但它们支持其他实现不支持的特殊字符串操作
• 由于Trie是按字符存储的，因此很容易实现longestPrefixOf和keysWithPrefix
• keysWithPrefix允许存在诸如自动完成之类的算法，可以通过使用优先队列进行优化。

key type	get(x)	add(x)
Balanced BST	comparable	Θ(logN)	Θ(logN)
RSC Hash Table	hashable	Θ(1)†	Θ(1)∗†
Data Indexed Array	chars	Θ(1)	Θ(1)
Tries (BST, HT, DICM)	Strings	Θ(1)Θ(1)	Θ(1)

*: Indicates “on average”.

†: Assuming items are evenly spread.

More generally, we can sometimes take special advantage of our key type to improve our sets and maps.

• Example: Tries handle String keys. Allow for fast string specific operations.

• Note: There are many other types of string sets/maps out there.

• • Suffix Trees (Link).

  • DAWG (Link).