目前关于图的问题

Problem	Problem Description	Solution	Efficiency
paths	Find a path from s to every reachable vertex.	DepthFirstPaths.javaDemo	O(V+E) timeΘ(V) space
shortest paths	Find the shortest path from s to every reachable vertex.	BreadthFirstPaths.javaDemo	O(V+E) timeΘ(V) space
shortest weighted paths	Find the shortest path, considering weights, from s to every reachable vertex.	DijkstrasSP.javaDemo	O(E log V) timeΘ(V) space
shortest weighted path	Find the shortest path, consider weights, from s to some target vertex	A*: Same as Dijkstra’s but with h(v, goal) added to priority of each vertex.Demo	Time depends on heuristic.Θ(V) space
minimum spanning tree	Find a minimum spanning tree.	LazyPrimMST.javaDemo	O(???) timeΘ(???) space
minimum spanning tree	Find a minimum spanning tree.	PrimMST.javaDemo	O(E log V) timeΘ(V) space
minimum spanning tree	Find a minimum spanning tree.	KruskalMST.javaDemo	O(E log E) timeΘ(E) sp

拓扑排序与DAG

拓扑排序

假设我们收集了不同的任务或活动，其中一些任务或活动必须在另一个任务或活动之前发生。我们如何找到对任务的排序，以便对于每个任务 v ，之前 v 发生的任务在我们的排序中更早出现？

我们可以首先将任务集合视为一个图，其中每个节点代表一个任务。边v→w 表示 v 必须在 w 之前发生。现在，我们原来的问题被简化为找到一个拓扑排序。

拓扑排序：对图的顶点进行排序，使得对于每个有向边 u→v ， u 在排序中都排在前面 v 。

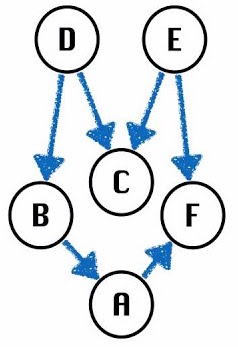
问题 1.1：上图有哪些有效的拓扑顺序？
答：[D,B,A,E,C,F], [E,D,C,B,A,F].

需要注意的是，只有对某些类型的图进行拓扑排序才有意义。若要查看此内容，请考虑下图：

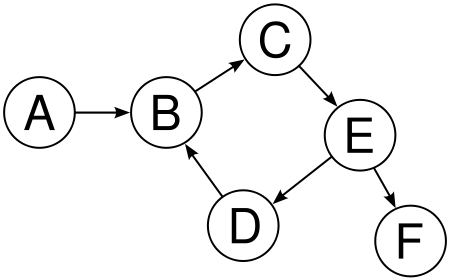
什么是有效的拓扑排序？

没有一个！D 在 B 之前，但 B 在 C、E、D 之前。由于我们有一个循环，因此没有定义拓扑排序。我们也不能对无向图进行拓扑排序，因为无向图中的每条边都会创建一个循环。

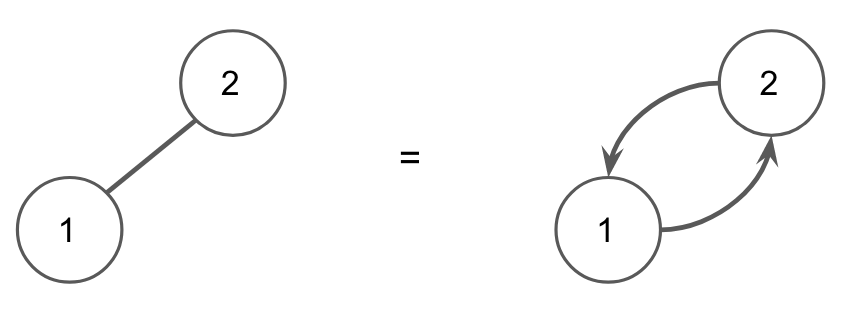
因此，拓扑排序仅适用于有向、无环（无周期）图或 DAG。

*Topological Sort:*：对 DAG 顶点的排序，使得对于每个有向边 u→*v ， u 在排序中排在前面 v 。

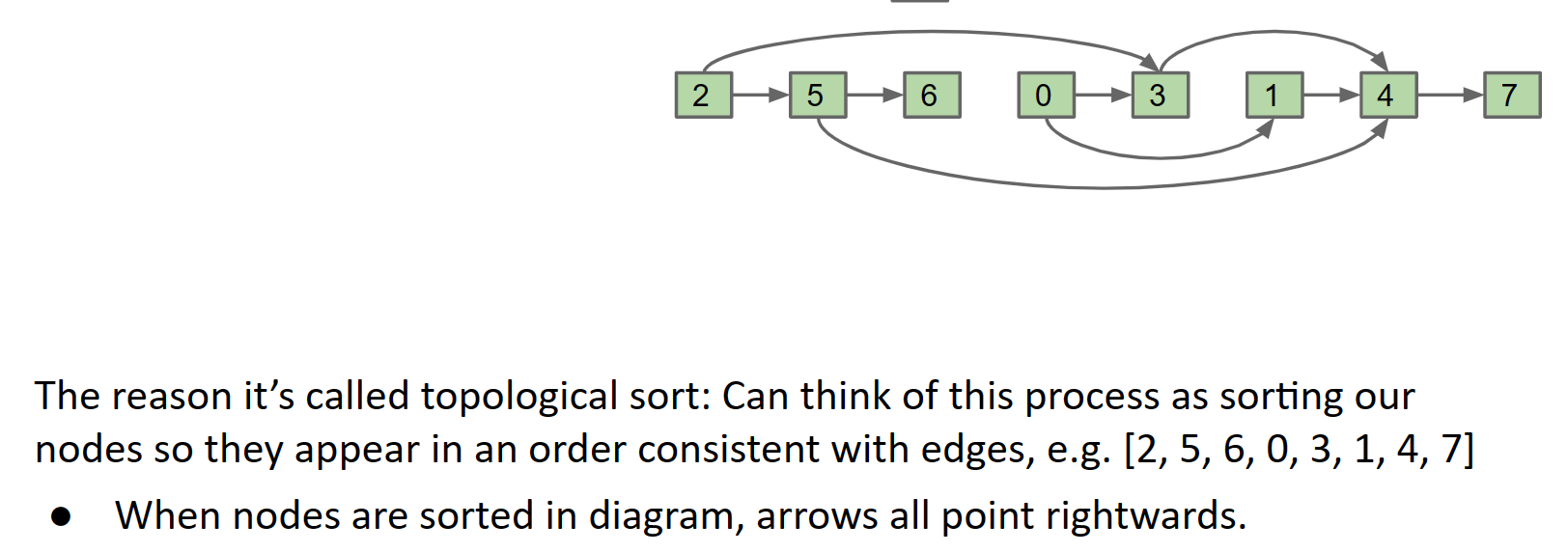
对于任何拓扑排序，都可以重新绘制图形，使顶点全部位于一行中。因此，拓扑排序有时称为图的线性化。例如，下面是针对其中一个拓扑排序线性化的前面示例。

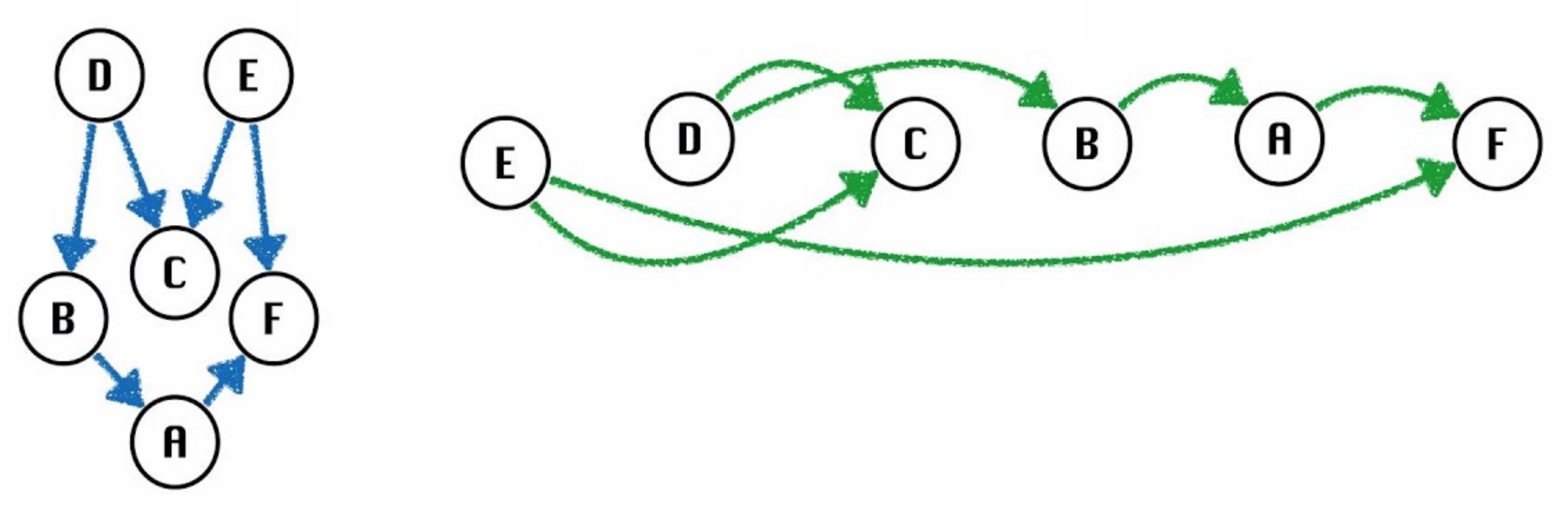
请注意，上述 DAG 的拓扑排序必须以 D 或 E 开头，并且必须以 F 或 C 结尾。因此，D 和 E 称为源，F 和 C 称为接收器。

拓扑排序算法

我们怎样才能找到拓扑排序？花点时间想想你已经知道的现有图算法可能有助于解决这个问题。

拓扑排序算法：

从图形中的每个顶点执行 DFS 遍历，而不是清除遍历之间的标记。
在此过程中记录 DFS 的后序。
拓扑顺序与后顺序相反。

工作原理：只有在考虑了给定源点的所有后代之后，每个顶点 v 才会被添加到后排序列表的末尾 v 。因此，当任何一个 v 被添加到后排序列表中时，它的所有后代都已经在列表中。因此，颠倒此列表会给出拓扑排序。

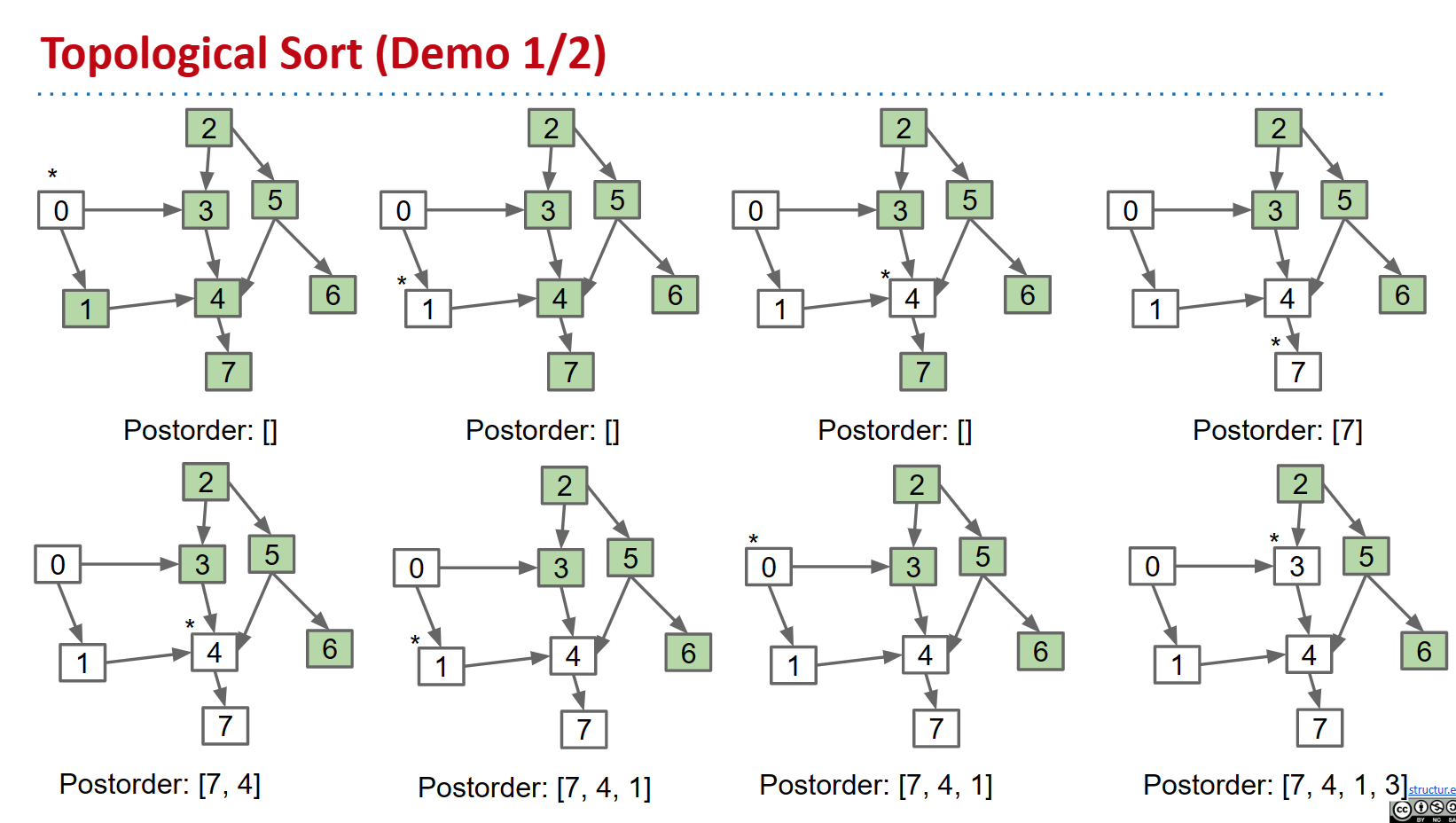
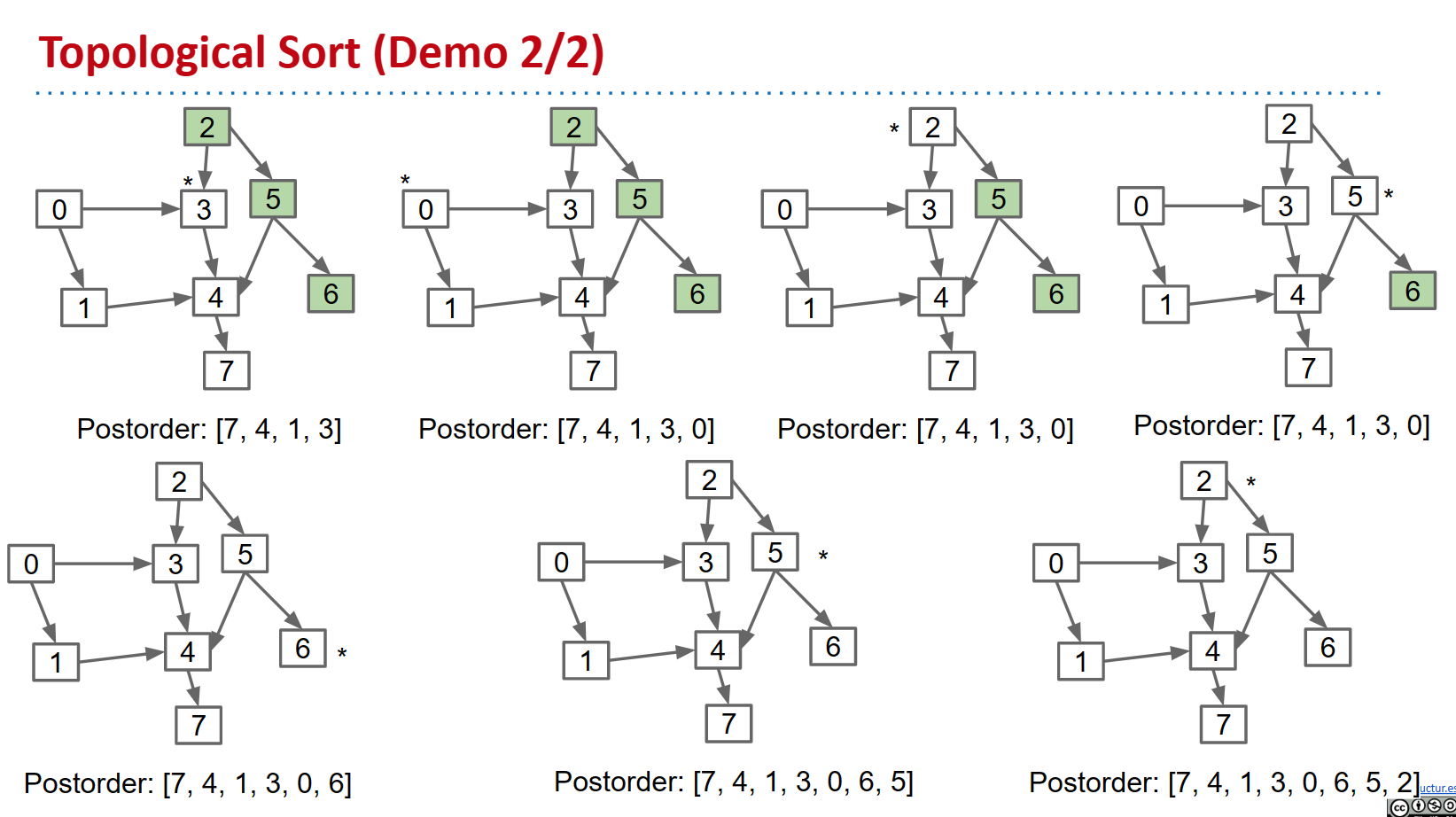
由于我们只是使用 DFS，因此它的运行时分别是 O(V+E) ，V E 是图中的节点数和边数。

Pseudocode 伪代码

topological(DAG):
    initialize marked array
    initialize postOrder list
    for all vertices in DAG:
        if vertex is not marked:
            dfs(vertex, marked, postOrder)
    return postOrder reversed

dfs(vertex, marked, postOrder):
    marked[vertex] = true
    for neighbor of vertex:
        dfs(neighbor, marked, postOrder)
    postOrder.add(vertex)

（超出范围）额外的问题：我们如何使用 BFS 实现拓扑排序？提示 1：我们肯定需要存储一些额外的信息。提示 2：考虑跟踪每个顶点的度数。

Solution: ：

计算所有顶点的度数。
选取任何 in-degree 为 0 的顶点 v 。
添加到 v 我们的拓扑排序列表。移除顶点 v 和从顶点出来的所有边。将顶点 v 的所有相邻项的度数递减 1。
重复步骤 2 和 3，直到删除所有顶点。

我们如何才能有效地完成第 2 步？我们可以使用优先级等于度数的顶点的最小优先级队列。

Review 回顾

拓扑排序是一种线性化有向无环图(DAG) 的方法。
我们可以使用 DFS（或 BFS）在 O*(V+*E) 时间内找到任何 DAG 的拓扑类型。
Problem Problem Description Solution Efficiency

topological sort Find an ordering of vertices that respects edges of our DAG. DemoTopological.java O(V+E) timeΘ(V) space

Problem	Problem Description	Solution	Efficiency
topological sort	Find an ordering of vertices that respects edges of our DAG.	DemoTopological.java	O(V+E) timeΘ(V) space

DAG上的最短路径

回想一下上一节，DAG 是有向的无环图。如果我们想在 DAG 上找到最短的路径，我们可以使用 Dijkstra 的路径。但是，对于 DAG，有一个简单的最短路径算法，它也可以处理负边权重！

Dijkstra 的负边权重失效

回想一下，如果存在负边，Dijkstra 可能会失败，因为它依赖于这样的假设，即一旦我们访问一条边，我们就找到了通往该边的最短路径。但是，如果负边权重可以存在于我们可以看到的地方之前，那么这个假设就失败了。请看以下示例：

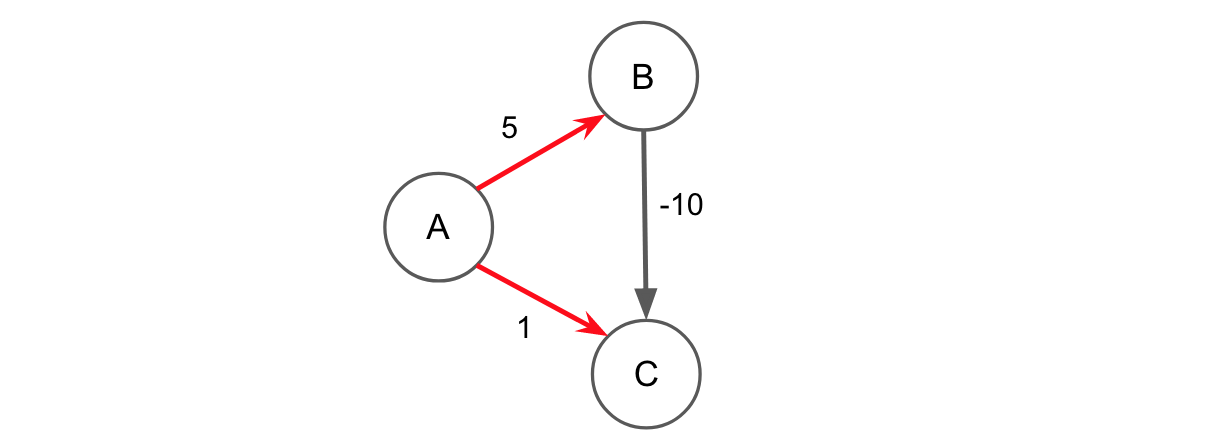
从 A 开始，Dijkstra 将首先访问 C，然后是 B（甚至从不考虑边缘 B→C* ）

当然，负边缘权重并不意味着 Dijkstra 一定会失败。Dijkstra’s 通过以下示例成功：

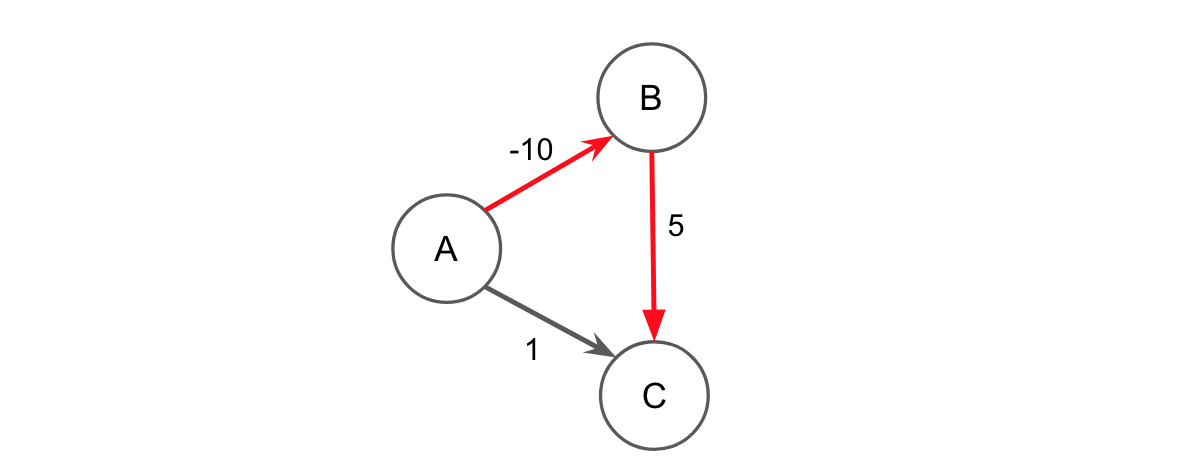
从技术上讲，这取决于您对 Dijkstra 的实现。如果我们确保放宽步骤只考虑仍在队列中（尚未访问）的邻居，那么确实 B→C* 永远不会考虑。如果你没有这个检查，那么从技术上讲，当我们从队列中弹出最后一个节点（B）时，我们会考虑B的邻居并更新C，这为我们提供了这个特定示例的正确答案。然而，在这种情况下，人们可能会争辩说该图打破了 Dijkstra 不变量，因此 Dijkstra 已经“失败”。请注意，Dijkstra 不变性：一旦从队列中删除一个节点（访问），您就找到了该节点的最短路径。

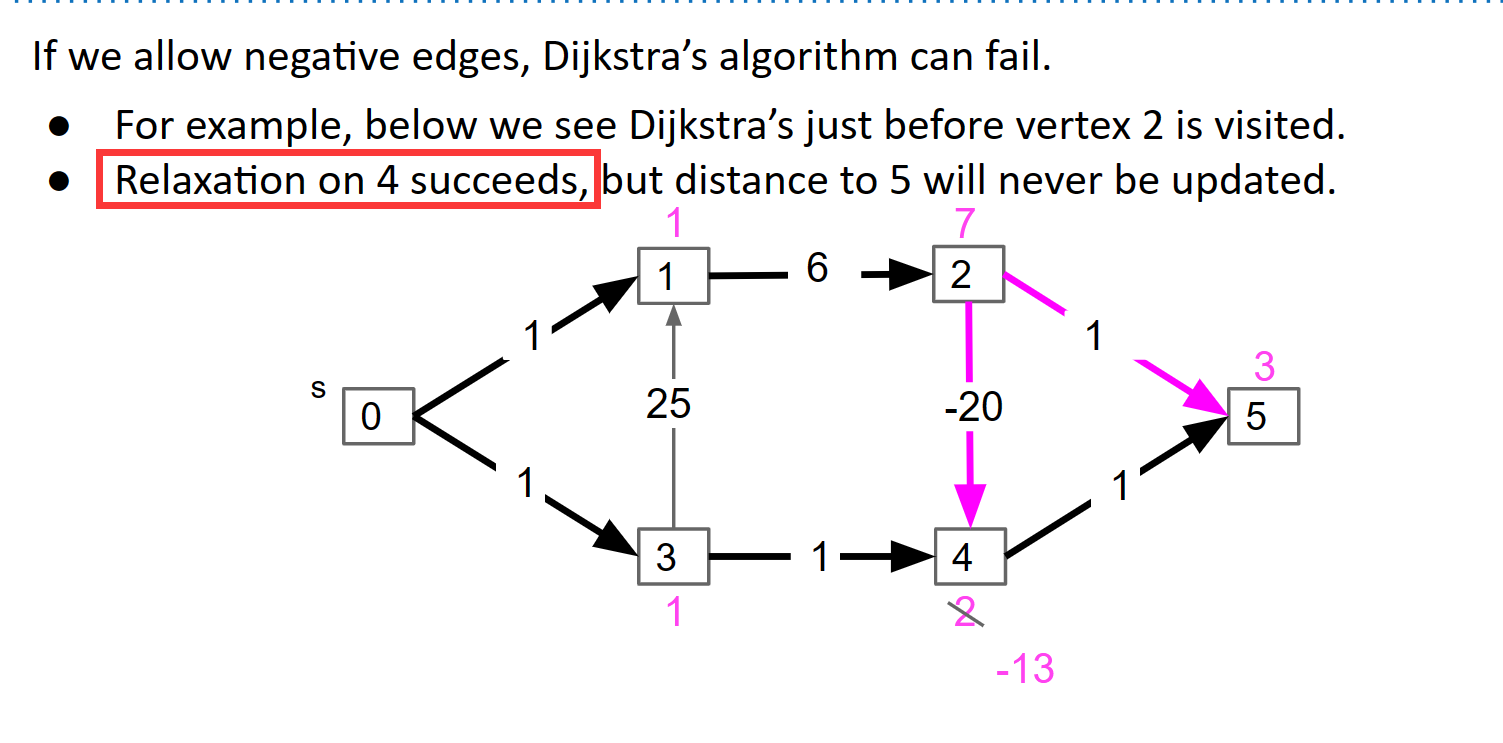
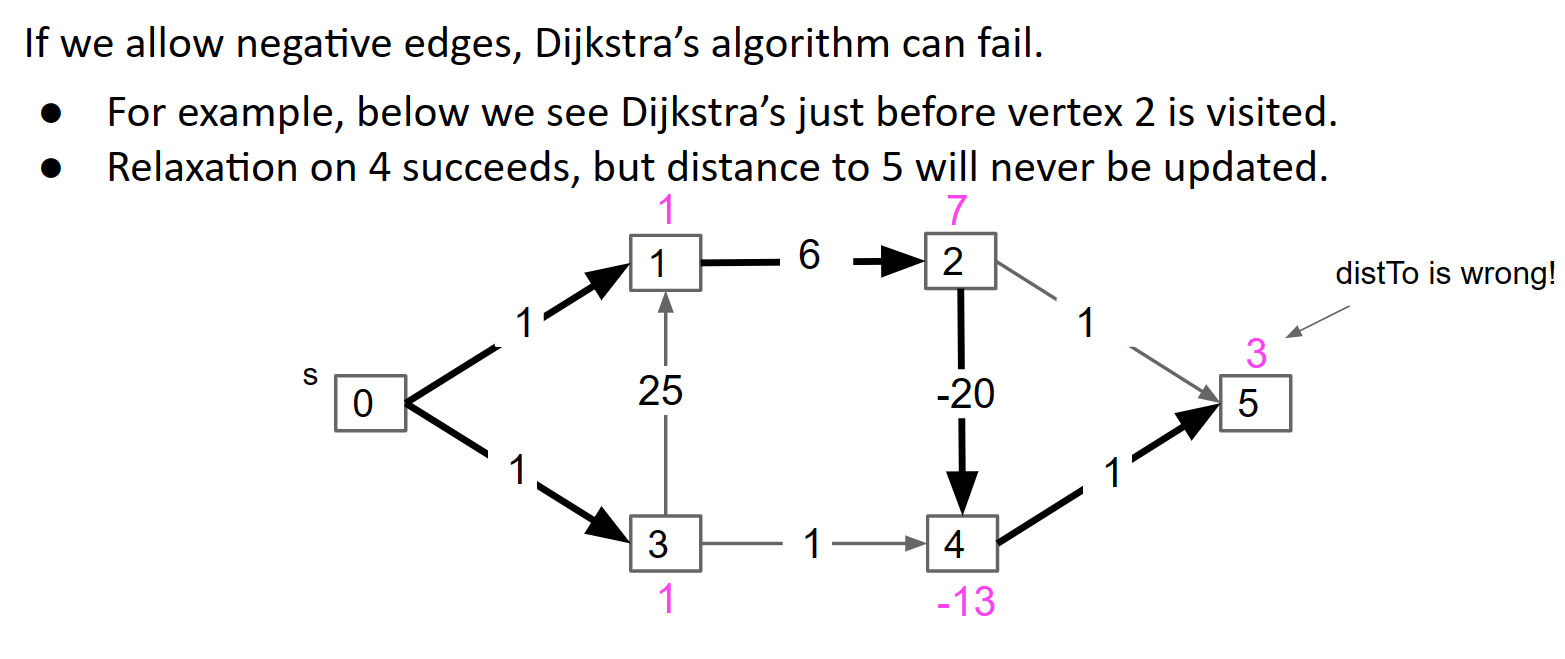
DAG 的最短路径算法

按拓扑顺序访问顶点：

每次访问时，释放所有外向的边缘

回想一下用重量 w 释放边缘u→v 的定义：

1
2
3

if distTo[u] + w < distTo[v]:
    distTo[v] = distTo[u] + w
    edgeTo[v] = u

由于我们按拓扑顺序访问顶点，因此只有在考虑了有关顶点的所有可能信息后，才会访问顶点。这意味着，如果负边权重存在于通往 v 的路径上，那么当我们到达 v ！

找到拓扑排序需要 O(V+E) 时间，而每个顶点的松弛也需要总共时间 O(V+E) 。因此，整个运行时为 O(V+E) 。回想一下，Dijkstra 需要 O((V+E)logV) 时间，因为我们的最小堆操作。

如果我们想解决不是 DAG 并且可能具有负边的图上的最短路径问题，该怎么办？Dijkstra 的扩展称为 Bellman Ford 可以满足您的需求，尽管它超出了本课程的范围。

Problem	Problem Description	Solution	Efficiency
topological sort	Find an ordering of vertices that respects edges of our DAG.	DemoCode: Topological.java	O(V+E) timeΘ(V) space
DAG shortest paths	Find a shortest paths tree on a DAG.	DemoCode: AcyclicSP.java	O(V+E) timeΘ(V) space

最长路径

通常

考虑查找从起始顶点到其他每个顶点的最长路径的问题。路径必须简单（不包含循环）。

事实证明，最著名的算法是指数级的（不切实际的低效）。

取负所有的边缘权重并找到最短路径会让我们处于一个棘手的境地，因为这样我们可能会有负循环，我们可能无限期地绕过它们。

DAG 上的最长路径

但是，如果我们处理的是 DAG，该怎么办？在这种情况下，我们没有循环，因此我们可以按照上面的建议进行操作：

形成图形的新副本，称为 G’，所有边权重均被否定（符号翻转）。
在 G’ 上运行 DAG 最短路径，得到结果 X
翻转 X.distTo 中所有值的符号。X.edgeTo 已经正确。

或者，我们可以修改上一节中的 DAG 最短路径算法，以在松弛边时选择较大的 distTo。虽然这在实践中更有意义，但考虑第一种方法的好处是能够将现有算法用作”black box“来解决新问题。我们将在下一节中详细了解此类问题解决： Reductions.

还原和分解

回想一下在上一节中，为了解决一个问题（最长路径），我们创建了一个新的图形 G’ 并将其输入到不同的算法中，然后解释结果。

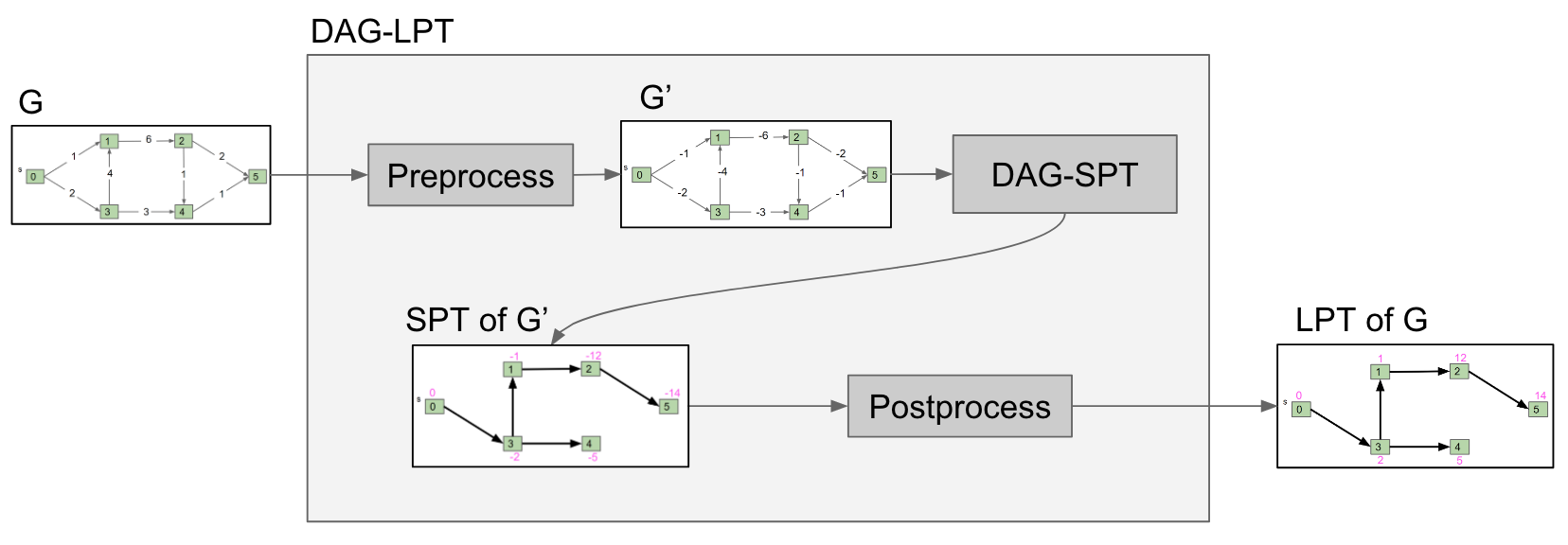
这个过程称为reduction还原。由于 DAG-SPT 可用于求解 DAG-LPT，因此我们说“DAG-LPT 简化为 DAG-SPT”。

换句话说，DAG-LPT的问题可以简化为DAG-SPT的问题。

像 DAG-LPT 这样的问题可能会简化为多个其他问题。作为现实世界的类比，考虑爬山。有很多方法可以解决“爬山”的问题。

“爬山”简化为“乘坐滑雪缆车”
“爬山”沦为“被大炮射出”
爬山”简化为“骑自行车上山”

从形式上讲，如果任务 Q 的任何子程序都可以用来求解 P，我们说 P 简化为 Q。

此定义可视化如下：

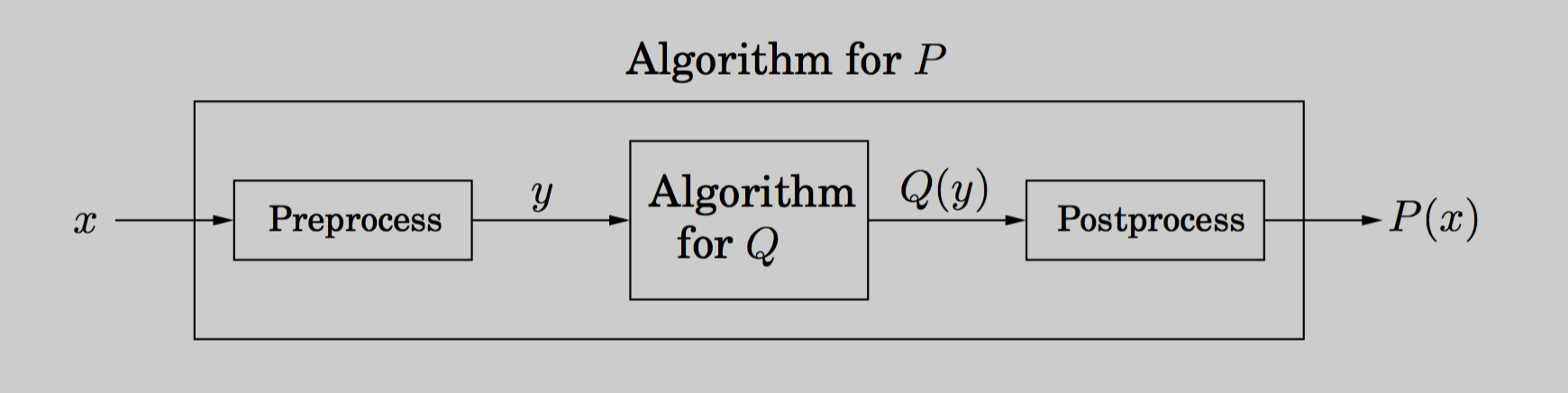
请注意，这只是本页第一个图形的概括。P 简化为 Q，因为 Q 用于求解 P。其工作原理是将输入 x 预处理成 y ，运行算法 Q 到 y ，并将输出后处理成 P 的解。这就是我们将 DAG-LPT 简化为 DAG-SPT 的方法。

Reflection 反射

可以说，我们在整个过程中一直在reduction。

Abstract Lists reduce to arrays or linked lists
摘要列表简化为数组或链表
Percolation reduces to Disjoint Sets
渗流减少到不相交集
Maze generation reduces to [your solution here ;)]
迷宫生成减少到 [您的解决方案在这里;)]

但是，这些并不完全是减少，因为您没有使用其他单一算法来解决您的问题。值得注意的是，在前面的约简示例中，我们使用独立集算法作为’black box‘来解决 3SAT。

对于我们在课程前面所完成的工作来说，也许一个更好的术语是decomposition分解 - 将复杂的任务分解成更小的部分。使用抽象使解决问题更容易。这是计算机科学的核心。