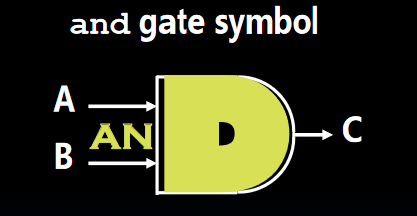
CS61C学习笔记(八)-组合逻辑
组合逻辑(Combinational_Logic)电路没有状态和记忆,某些输入集的输出总是相同。
真值表(Truth Tables/TT)
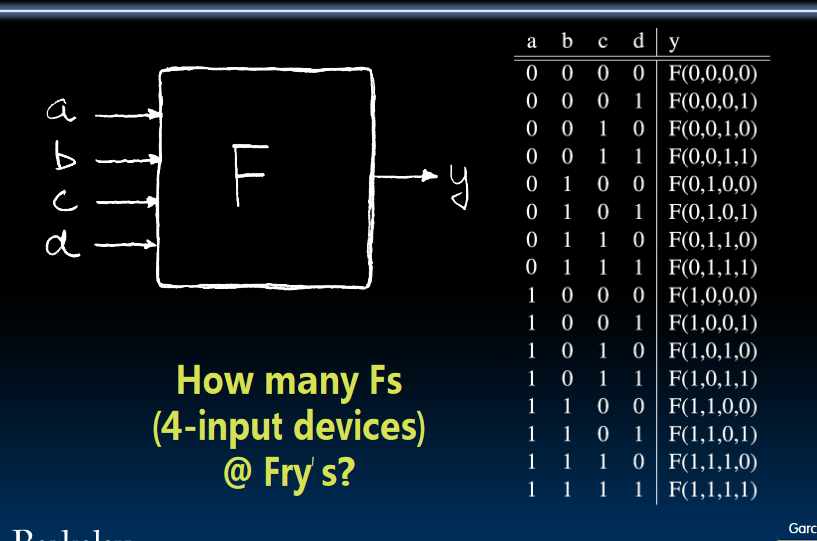
TT Example #1: 1 iff one (not both) a,b=1
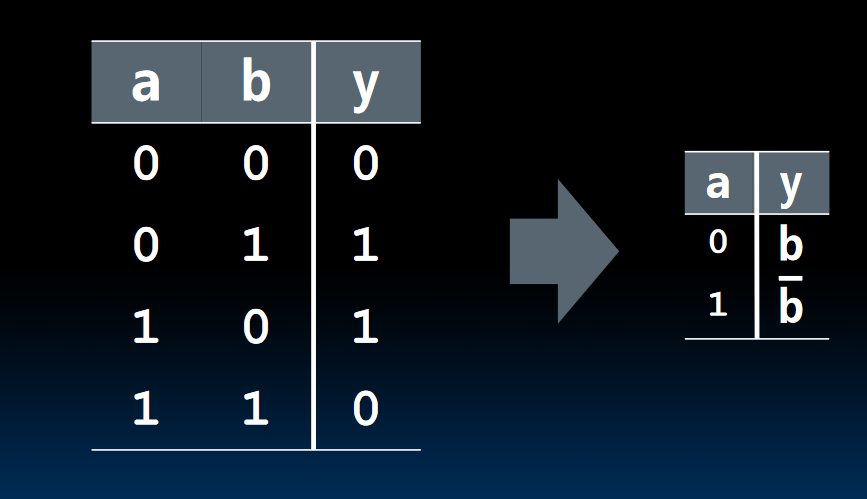
这个也是后面会说到的XOR,trick xor treat!
使用a和b的关系简化真值表:
- 当a为0时,输出y等于b。
- 当a为1时,输出y等于not b。
TT Example #2: 2-bit adder
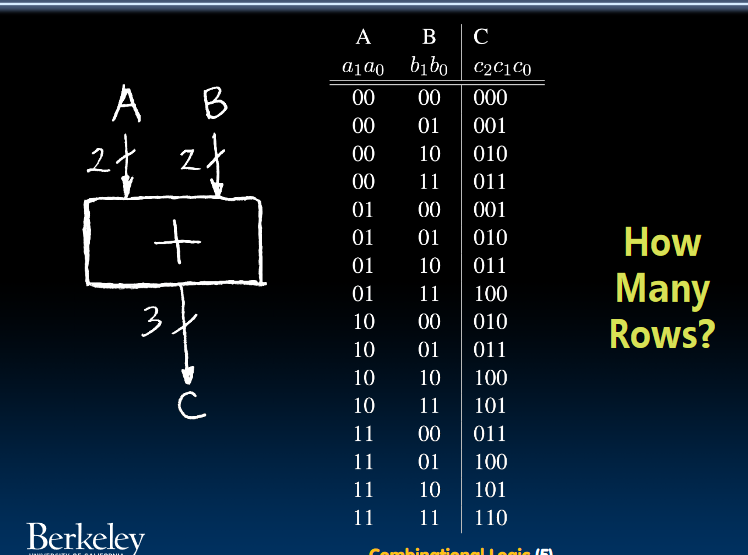
输入A和B分别有两位,输出C有三位(包括进位)。
总共需要16行(4位输入)。
TT Example #3: 32-bit unsigned adder

输入A和B分别有32位,输出C需要33位(包括进位)。
真值表的方法在这种情况下可能不适用,需考虑其他构建方法。
TT Example #4: 3-input majority circuit
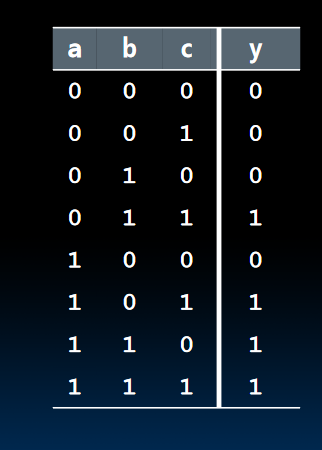
逻辑门

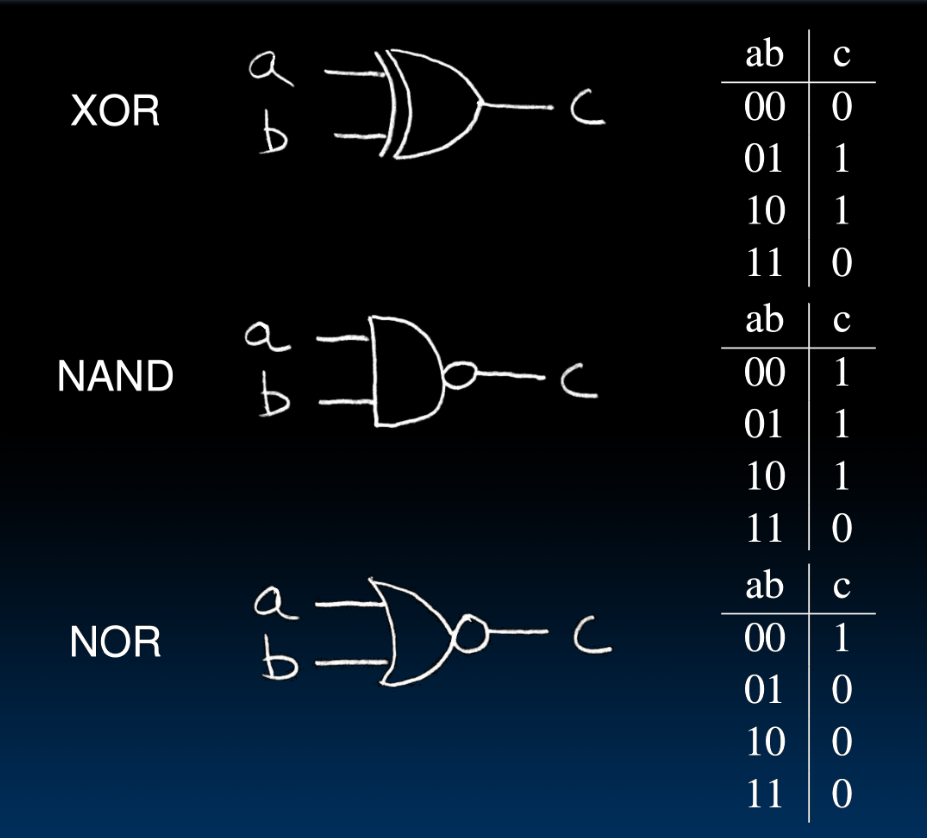
如何记忆:
2-input gates extend to n-inputs

对于XOR的N-input数abc中有多少个1,奇数个1最终结果就是1
Truth Table -> Gates (e.g., majority circ.)
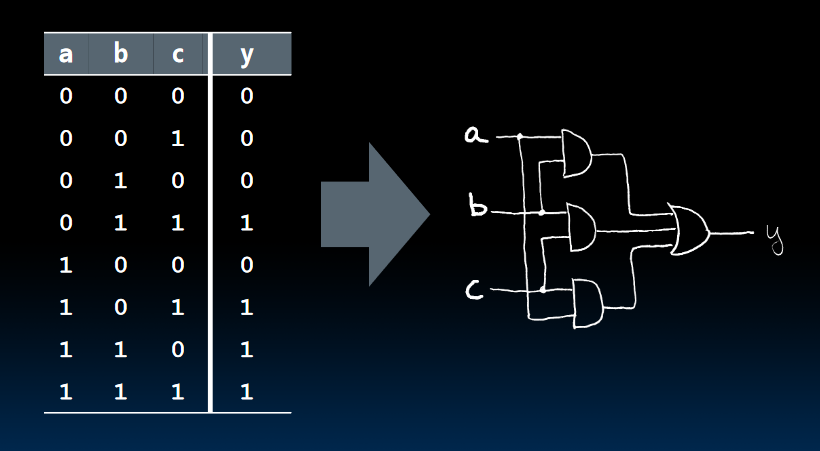
Truth Table -> Gates (e.g., FSM circuit)
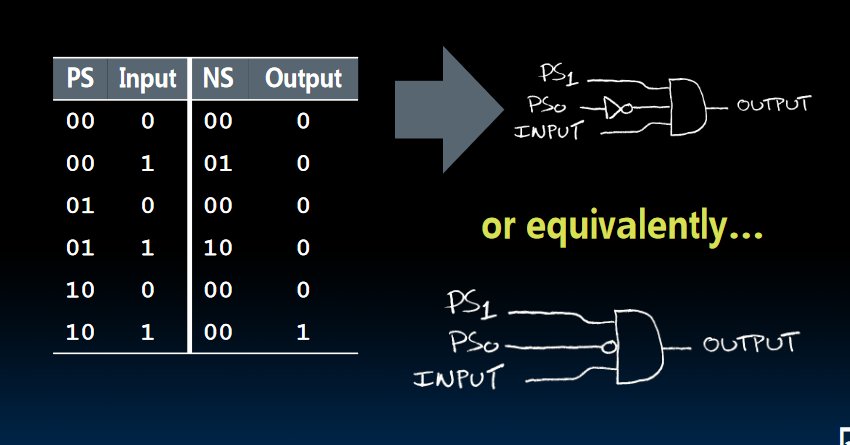
布尔代数

+=OR·=AND- $\bar{x}$ =
NOT
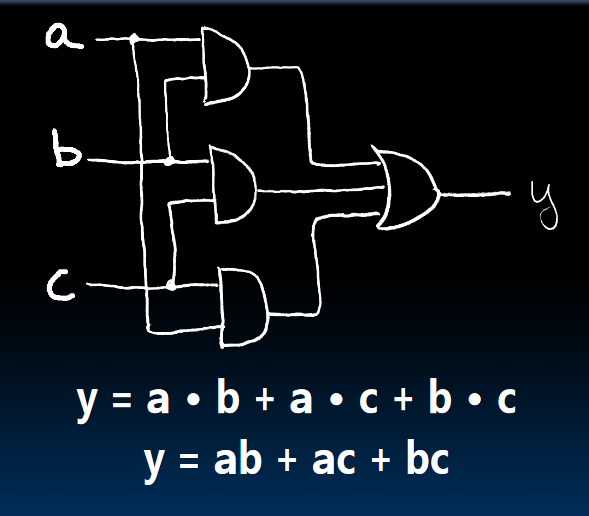
Boolean Algebra (e.g., for majority fun.)
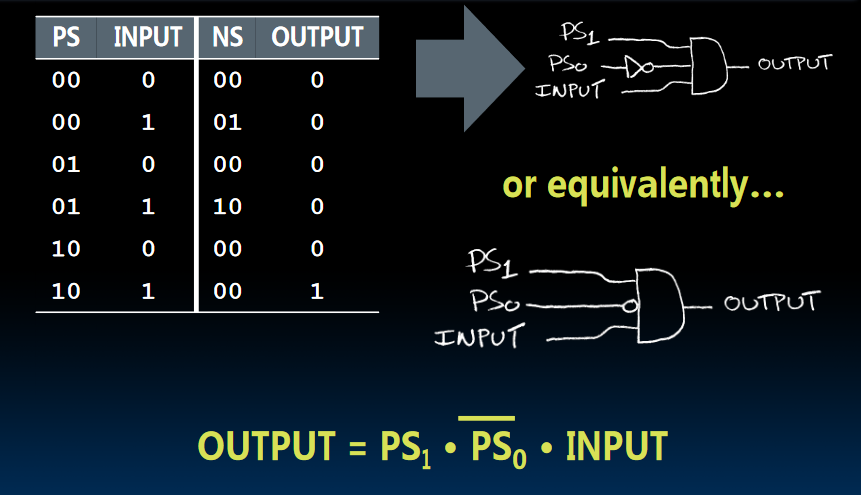
Boolean Algebra (e.g., for FSM)
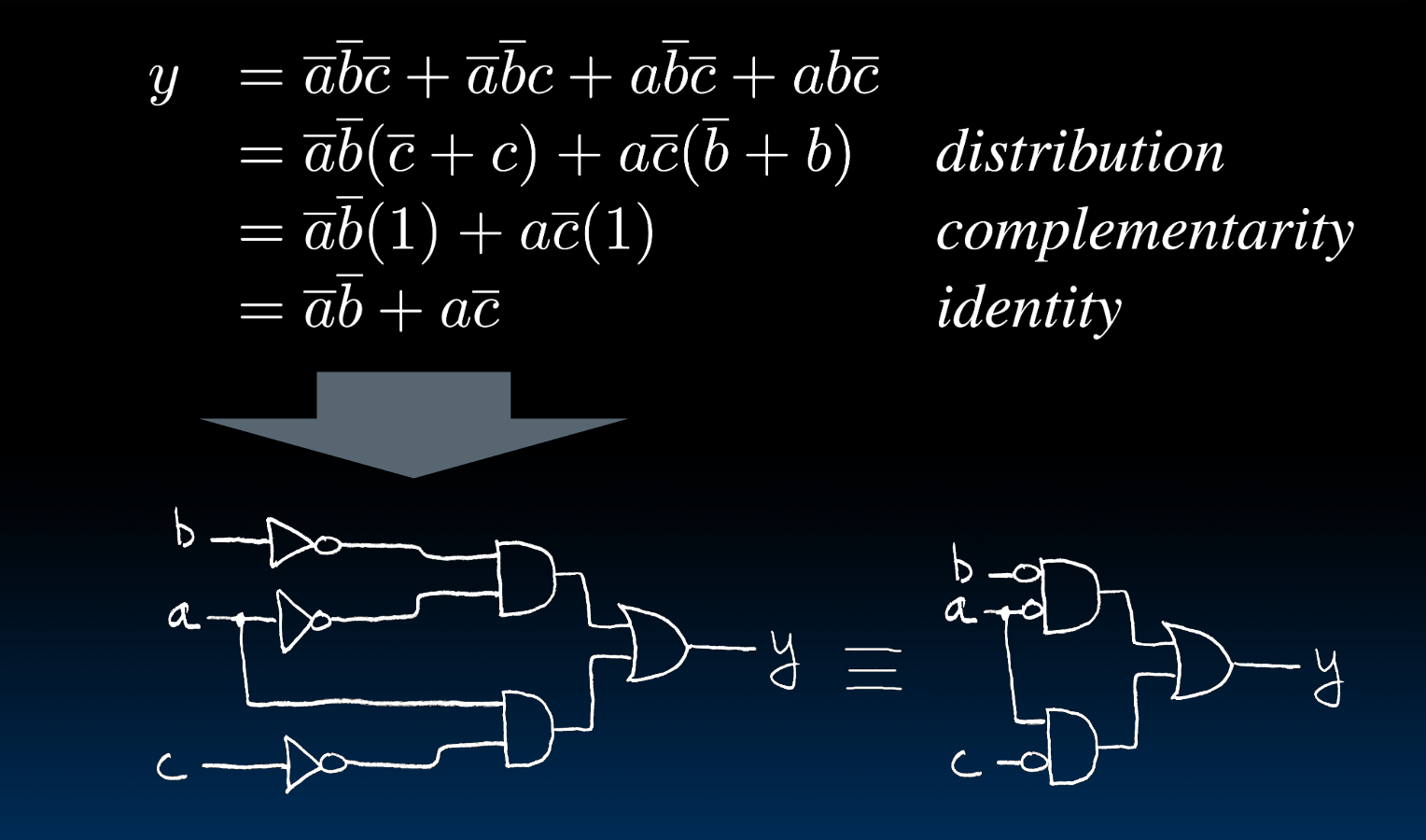
电路&代数简化

布尔代数的规则
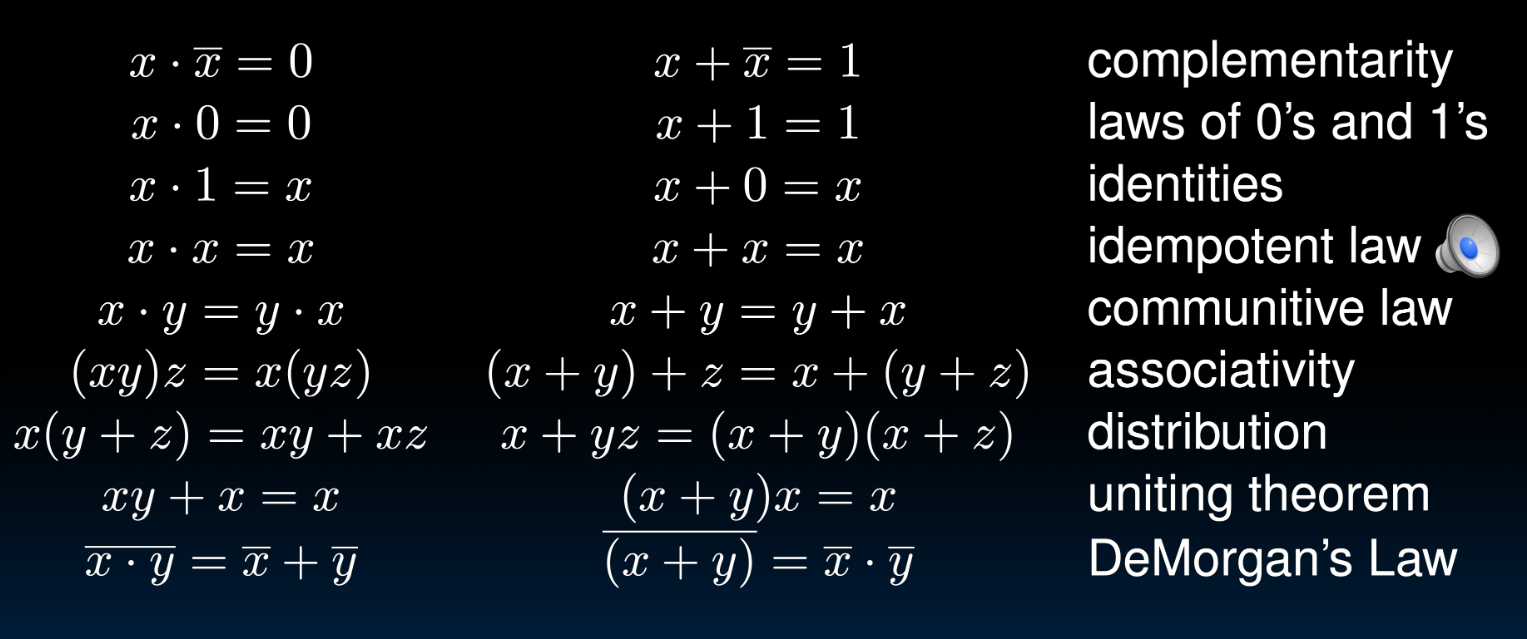
标准型(Canonical forms)

总结
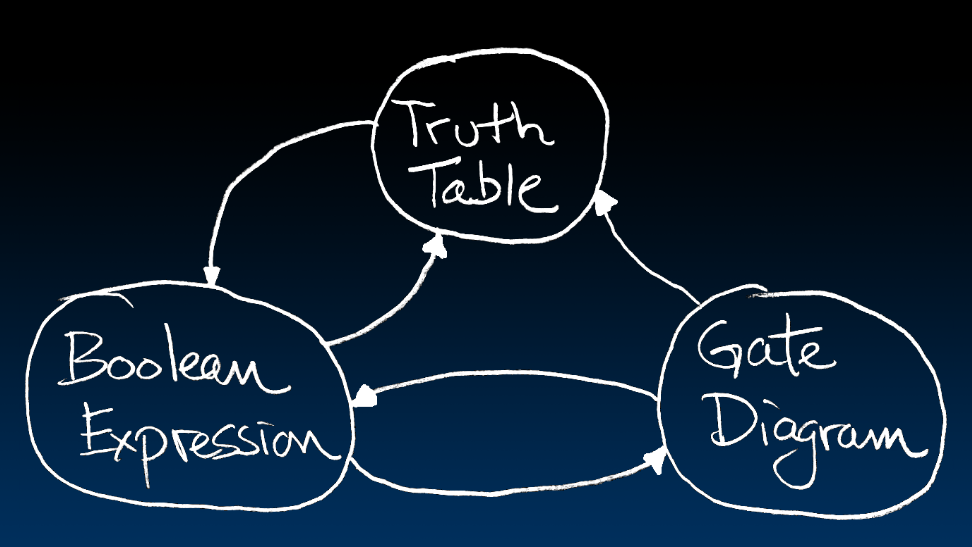
我们可以互相转化,除了TT转成GD
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 云泥小窝!
评论